
【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④![]() .其中一定成立的是( )
.其中一定成立的是( )
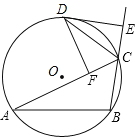
A.①②③B.②③④C.①③④D.①②④
【答案】D
【解析】
①易证△CDE≌△CDF,得CE=CF;
②∠ACB+∠ACE=180°,根据四边形内角和定理得∠ACE+∠EDF=180°,所以∠ACB=∠EDF;
③无法证明DE是切线;
④根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,所以∠DAB=∠DCA,根据圆周角定理判断![]() .
.
解:①∵∠DCE=∠DCF,∠DEC=∠DFC,DC=DC,
∴△CDE≌△CDF,得CE=CF.故成立;
②∵∠ACB+∠ACE=180°,
根据四边形内角和定理得∠ACE+∠EDF=180°,
∴∠ACB=∠EDF,故成立;
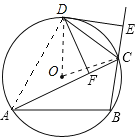
③连接OD、OC.则∠ODC=∠OCD.
假如DE是切线,则OD⊥DE,
∵BE⊥DE,
∴OD∥BE,∠DCE=∠ODC=∠OCD,
而∠DCE=∠DCA,∠OCD≠∠DCA,
故DE不是切线;
④连接AD,根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,
∴∠DAB=∠DCA,根据圆周角定理判断弧AD=弧BD.故成立.
故选:D.


 新课标同步训练系列答案
新课标同步训练系列答案科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,其中
,其中![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
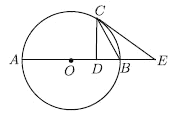
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)如图,点![]() 在
在![]() 上,且满足
上,且满足![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
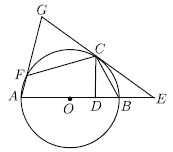
①试探究线段![]() 与
与![]() 之间满足的数量关系.
之间满足的数量关系.
②若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小蓉从格致楼底楼点A处沿立人大礼堂旁的台阶AB拾阶而上,步行20米后到达万象楼楼底点B,再从点B直线行进15米到达直通博雅楼的台阶底端C,然后沿台阶CD步行至博雅楼底楼的小平台D.在D点处测得竖立于百汇园旁的万象楼BE的楼顶点E的仰角为30°.如图所示,已知台阶AB与水平地面夹角为45°,台阶CD与水平地面夹角为60°,CD=12米,点A,B,C,D,E在同一平面.则格致楼楼底点A到万象楼楼顶点E的垂直高度约为( )(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
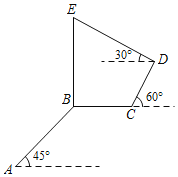
A.22.1米B.35.2米C.27.3米D.36.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
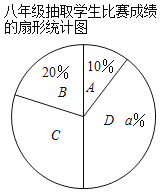
【题目】为加强学生对“垃圾分类知识”的重视程度,某学校组织了“垃圾分类知识”比赛.现七、八年级各抽取10名同学的成绩进行统计分析(成绩得分用x表示,共分成四组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100),绘制了如下的图表,请根据图中的信息解答下列问题:
七年级10名学生的成绩是:69,78,96,77,68,95,86,100,85,86
八年级10名学生的成绩在C组中的数据是:86,87,87
七、八年级抽取学生比赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84 | 85.5 | b | 109.6 |
八年级 | 84 | c | 92 | 102.6 |
(1)直接写出上述图表中a,b,c的值:a= ,b= ,c= .
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(一条理由即可): .
(3)若两个年级共680人参加了此次比赛,估计参加此次比赛成绩优秀(90≤x≤100)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
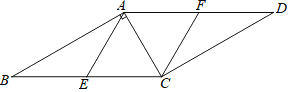
【题目】如图,已知点E,F分别是平行四边形ABCD的边BC,AD上的中点.
(1)AE与CF的关系是 ,请证明;
(2)若∠BAC= °时,四边形AECF是菱形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x+5经过点A,C.
(1)求抛物线的解析式;
(2)如图(2),若过点B的直线交直线AC于点M.
①当BM⊥AC时,过抛物线上一动点P(不与点B,C重合),作直线BM的平行线交AC于点Q,若以点B,M,Q,P为顶点的四边形是平行四边形,求点P的横坐标;
②连结BC,当直线BM与直线AC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com