
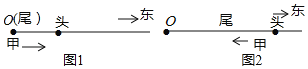
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() ,此时队伍在此过程中行进的路程为
,此时队伍在此过程中行进的路程为![]() .
.
【解析】
(1)①排头与O的距离为S头(m).等于排头行走的路程+队伍的长300,而排头行进的时间也是t(s),速度是2m/s,可以求出S头与t的函数关系式;
②甲赶到排头位置的时间可以根据追及问题的数量关系得出,代入求S即可;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m)是在S的基础上减少甲返回的路程,而甲返回的时间=总时间t-甲从排尾赶到排头的时间,于是可以求S甲与t的函数关系式;
(2)甲这次往返队伍的总时间为T(s),是甲从排尾追到排头用的时间与从排头返回排尾用时的和,可以根据追及问题和相遇问题的数量关系得出结果;在甲这次往返队伍的过程中队伍行进的路程=队伍速度×返回时间.
(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),∴S头=2t+300;
②甲从排尾赶到排头的时间为300÷(2v﹣v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m,甲返回时间为:(t﹣150)s,∴S甲=S头﹣S甲回=2×150+300﹣4(t﹣150)=﹣4t+1200;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S的值为600m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=﹣4t+1200.
(2)T=t追及+t返回![]() ,在甲这次往返队伍的过程中队伍行进的路程为:v
,在甲这次往返队伍的过程中队伍行进的路程为:v![]() 400;
400;
因此T与v的函数关系式为:T![]() ,此时队伍在此过程中行进的路程为400m.
,此时队伍在此过程中行进的路程为400m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
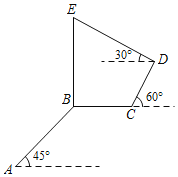
【题目】小蓉从格致楼底楼点A处沿立人大礼堂旁的台阶AB拾阶而上,步行20米后到达万象楼楼底点B,再从点B直线行进15米到达直通博雅楼的台阶底端C,然后沿台阶CD步行至博雅楼底楼的小平台D.在D点处测得竖立于百汇园旁的万象楼BE的楼顶点E的仰角为30°.如图所示,已知台阶AB与水平地面夹角为45°,台阶CD与水平地面夹角为60°,CD=12米,点A,B,C,D,E在同一平面.则格致楼楼底点A到万象楼楼顶点E的垂直高度约为( )(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
A.22.1米B.35.2米C.27.3米D.36.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x+5经过点A,C.
(1)求抛物线的解析式;
(2)如图(2),若过点B的直线交直线AC于点M.
①当BM⊥AC时,过抛物线上一动点P(不与点B,C重合),作直线BM的平行线交AC于点Q,若以点B,M,Q,P为顶点的四边形是平行四边形,求点P的横坐标;
②连结BC,当直线BM与直线AC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
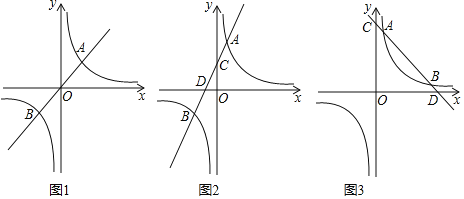
【题目】如图1,直线y=x与双曲线y=![]() 交于A,B两点,根据中心对称性可以得知OA=OB.
交于A,B两点,根据中心对称性可以得知OA=OB.
(1)如图2,直线y=2x+1与双曲线y=![]() 交于A,B两点,与坐标轴交点C,D两点,试证明:AC=BD;
交于A,B两点,与坐标轴交点C,D两点,试证明:AC=BD;
(2)如图3,直线y=ax+b与双曲线y=![]() 交于A,B两点,与坐标轴交点C,D两点,试问:AC=BD还成立吗?
交于A,B两点,与坐标轴交点C,D两点,试问:AC=BD还成立吗?
(3)如果直线y=x+3与双曲线y=![]() 交于A,B两点,与坐标轴交点C,D两点,若DB+DC≤5
交于A,B两点,与坐标轴交点C,D两点,若DB+DC≤5![]() ,求出k的取值范围.
,求出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
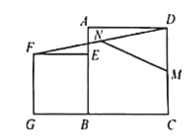
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com