
【题目】如图,在平面直角坐标系中,二次函数y=﹣ ![]() x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
【答案】
(1)
解:把A(0,8),B(﹣4,0)代入y=﹣ ![]() x2+bx+c得
x2+bx+c得 ![]() ,解得
,解得 ![]() ,
,
所以抛物线的解析式为y=﹣ ![]() x2+x+8;
x2+x+8;
当y=0时,﹣ ![]() x2+x+8=0,解得x1=﹣4,x2=8,
x2+x+8=0,解得x1=﹣4,x2=8,
所以C点坐标为(8,0)
(2)
解:①连结OF,如图,
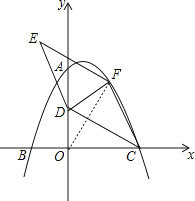
设F(t,﹣ ![]() t2+t+8),
t2+t+8),
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF﹣S△OCD= ![]() 4t+
4t+ ![]() 8(﹣
8(﹣ ![]() t2+t+8)﹣
t2+t+8)﹣ ![]() 48
48
=﹣t2+6t+16
=﹣(t﹣3)2+25,
当t=3时,△CDF的面积有最大值,最大值为25,
∵四边形CDEF为平行四边形,
∴S的最大值为50;
②∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣ ![]() t2+t+12),
t2+t+12),
∵E(t﹣8,﹣ ![]() t2+t+12)在抛物线上,
t2+t+12)在抛物线上,
∴﹣ ![]() (t﹣8)2+t﹣8+8=﹣
(t﹣8)2+t﹣8+8=﹣ ![]() t2+t+12,解得t=7,
t2+t+12,解得t=7,
当t=7时,S△CDF=﹣(7﹣3)2+25=9,
∴此时S=2S△CDF=18.
【解析】(1)把A点和B点坐标代入y=﹣ ![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标(2)①连结OF,如图,设F(t,﹣
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标(2)①连结OF,如图,设F(t,﹣ ![]() t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF , 利用三角形面积公式得到S△CDF=﹣t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值; ②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣
t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF , 利用三角形面积公式得到S△CDF=﹣t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值; ②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣ ![]() t2+t+12),然后把E(t﹣8,﹣
t2+t+12),然后把E(t﹣8,﹣ ![]() t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,掌握点平移的坐标规律.
t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,掌握点平移的坐标规律.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】文昌某校准备组织学生及学生家长到三亚进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上;根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元;已知学生家长与教师的人数之比为2:1,文昌到三亚的火车票价格(部分)如下表所示:
运行区间 | 公布票价 | 学生票 | ||
上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
文昌 | 三亚 | 81(元) | 68(元) | 51(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
B.y=﹣(x+ ![]() )2﹣
)2﹣ ![]()
C.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
D.y=﹣(x+ ![]() )2+
)2+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( ) 
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= ![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 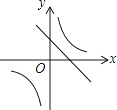
A.
B.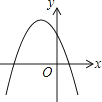
C.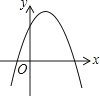
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com