
【题目】如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 ![]() 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.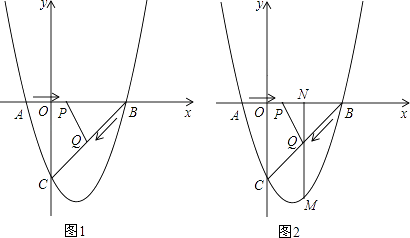
(1)求二次函数的解析式;
(2)如图1,当△BPQ为直角三角形时,求t的值;
(3)如图2,过点Q作QN⊥x轴于N,交抛物线于点M,连结MC,MB,当t为何值时,△MCB的面积最大,并求出此时点M的坐标和△MCB面积的最大值.
【答案】
(1)
解:∵二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,
∴抛物线的解析式为y=(x+1)(x﹣3),整理得:y=x2﹣2x﹣3.
(2)
解:∵当x=0时,y=﹣3,
∴C(0,﹣3).
∴OB=OC.
∴∠PBQ=45°.
如图1所示:当∠PQB=90°时.则PB= ![]() BQ.
BQ.
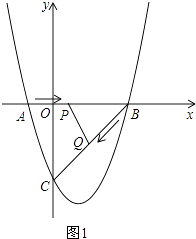
∵AP=t,BQ= ![]() t,AB=4,
t,AB=4,
∴AP+PB=t+2t=4.
∴t= ![]() .
.
如图2所示:当∠QPB=90°时.
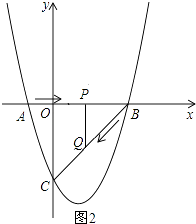
∵∠PBQ=45°,∠BPQ=90°,
∴PB= ![]() BQ=
BQ= ![]() ×
× ![]() t=t.
t=t.
∵AP=t,AB=4,
∴t+t=4.
解得:t=2.
综上所述,当t=2或t= ![]() 时,△BPQ为直角三角形.
时,△BPQ为直角三角形.
(3)
解:设直线BC的解析式为y=kx+b.
∵将C(0,﹣3)、B(3,0)代入得: ![]() ,解得:k=1,b=﹣3,
,解得:k=1,b=﹣3,
∴直线BC的解析式为y=x﹣3.
设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=a﹣3﹣(a2﹣2a﹣3)=﹣a2+3a.
∵S△BCM= ![]() OBQM=
OBQM= ![]() ×3(﹣a2+3a)=﹣
×3(﹣a2+3a)=﹣ ![]() (a2﹣3a)=﹣
(a2﹣3a)=﹣ ![]() (a﹣
(a﹣ ![]() )2+
)2+ ![]() ,
,
∴当a= ![]() 时,△BCM的面积的最大值为
时,△BCM的面积的最大值为 ![]() .
.
∴点P的坐标( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)由题意可知a=1,依据二次函数的交点式可知抛物线的解析式为y=(x+1)(x﹣3),然后整理即可;(2)分为∠PQB=90°和∠BPQ=90°两种情况求解.当∠PQB=90°时,PB= ![]() QB=2t,然后依据AB=AP+PB列方程求解即可;当∠BPQ=90°时,PB=
QB=2t,然后依据AB=AP+PB列方程求解即可;当∠BPQ=90°时,PB= ![]() QB=t,然后依据AB=AP+PB列方程求解即可;(3)先求得直线BC的解析式,然后设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=﹣a2+3a.由S△BCM
QB=t,然后依据AB=AP+PB列方程求解即可;(3)先求得直线BC的解析式,然后设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=﹣a2+3a.由S△BCM![]() OBQM,得到△BCN的面积与a的函数关系式,然后依据配方法可求得△BCN的面积的最大值以及点P的坐标.
OBQM,得到△BCN的面积与a的函数关系式,然后依据配方法可求得△BCN的面积的最大值以及点P的坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在进行二次根式的化简与运算时,如遇到 ![]() ,
, ![]() ,
, ![]() 这样的式子,还需做进一步的化简:
这样的式子,还需做进一步的化简:![]() =
= ![]() =
= ![]() .①
.①![]() =
= ![]() =
= ![]() .②
.②![]() =
= ![]() =
= ![]() =
= ![]() ﹣1.③
﹣1.③
以上化简的步骤叫做分母有理化.![]() 还可以用以下方法化简:
还可以用以下方法化简:![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ﹣1.④
﹣1.④
(1)请用不同的方法化简 ![]()
(I)参照③式化简 ![]() =
=
(II)参照④式化简 ![]()
(2)化简: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是( )
个单位长度,则第2019秒时,点P的坐标是( )

A. (2019,0) B. (2019,-1) C. (2019,1) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标是(-5,0),(-4,-2),(-3,0),(-2,-2),(-1,0)的点用线段依次连接起来形成一个图案Ⅰ.
(1)作出该图案关于y轴对称的图案Ⅱ;
(2)将所得到的图案Ⅱ沿x轴向上翻折180°后得到一个新图案Ⅲ,试写出它的各顶点的坐标;
(3)观察图案Ⅰ与图案Ⅲ,比较各顶点的坐标和图案位置,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),将△ABC绕原点O旋转180度得到△A1B1C1 . 结合所给的平面直角坐标系解答下列问题: 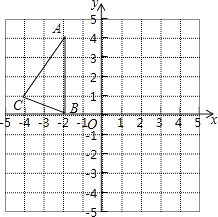
(1)画出△A1B1C1;
(2)画出一个△A2B2C2 , 使它分别与△ABC,△A1B1C1轴对轴(其中点A,B,C与点A2 , B2 , C2对应);
(3)在(2)的条件下,若过点B的直线平分四边形ACC2A2的面积,请直接写出该直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
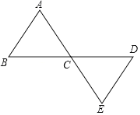
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )
A.45°
B.90°
C.120°
D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com