
【题目】如图,长方形![]() 中,点
中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标是
的坐标是![]() ,长方形
,长方形![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .
.
(1)求线段![]() 的长;
的长;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 在直线
在直线![]() 上,在
上,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请求出满足条件的点
为顶点的四边形是平行四边形?若存在,请求出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)BO=10;(2)点![]() 的坐标
的坐标![]() ;(3)存在.直线
;(3)存在.直线![]() 与
与![]() 轴的交点
轴的交点![]() ,0).
,0).
【解析】
(1)利用勾股定理计算即可.
(2)设![]() ,则
,则![]() ,
,![]() 在
在![]() 中,根据
中,根据![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(3)存在.过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则四边形
,则四边形![]() 为平行四边形.思想想办法求出点
为平行四边形.思想想办法求出点![]() 的坐标,再求出直线
的坐标,再求出直线![]() 的解析式即可解决问题.
的解析式即可解决问题.
解:(1)![]() 点
点![]() 的坐标是
的坐标是![]()
![]() ,
,![]()
![]() .
.
(2)由折叠可知:![]() ,
,![]()
设![]() ,则
,则![]() ,
,![]()
在![]() 中,
中,![]()
即![]()
解得:![]()
![]() 点
点![]() 的坐标
的坐标![]() .
.
(3)存在.过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则四边形
,则四边形![]() 为平行四边形.
为平行四边形.

在![]() 中,
中,![]() ,
,![]() ,
,![]() ,作
,作![]() ,垂足为
,垂足为![]()
则![]() ,
,![]() ,
,
解得:![]() ,
,
由勾股定理可解得:![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]()
![]() ,
,![]()
![]() 直线
直线![]() 的函数表达式为:
的函数表达式为:![]() ,
,
设直线![]() 的函数表达式为:
的函数表达式为:![]() ,
,
将点![]() 的坐标
的坐标![]() ,
,![]() 代入解得:
代入解得:![]()
![]() 直线
直线![]() 的函数表达式为:
的函数表达式为:![]() .
.
直线![]() 与
与![]() 轴的交点
轴的交点![]() ,0).
,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
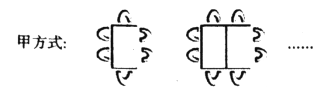
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
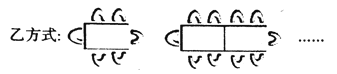
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣12+3×(﹣2)3﹣(﹣6)÷(﹣![]() )2;
)2;
(2)﹣2﹣12×(![]() );
);
(3)3x2+(2x2﹣3x)﹣(﹣x+5x2);
(4)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米;
(2)小明在书店停留了多少分钟;
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
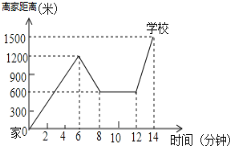
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了以“美好家园,你我共建;节能减排,人人有责”为主题的电子小报制作比赛,评分结果有60.70.80.90.100五种。现从中随机抽取部分作品,对其份数及成绩进行整理,制作如下两幅不完整的统计图。根据图中提供的信息,解答下列问题:
(1)本次抽取了多少份作品
(2)补全两幅统计图
(3)已知该校收取参赛作品共600份,请估计该校比赛成绩达到90分以上(含90分)的作品有多少份?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,点C(3,8),E、F为AB、CD边上的中点,如图1,点A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,点B随之沿y轴下滑,并带动矩形ABCD在平面内滑动,如图2,设运动时间表示为t秒,当点B到达原点时停止运动.
(1)当t=0时,点F的坐标为 ;
(2)当t=4时,求OE的长及点B下滑的距离;
(3)求运动过程中,点F到点O的最大距离;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com