
����Ŀ��ijУΪ���˽�ѧ���ҳ��Ժ���ʹ���ֻ���̬������������ȡ����ѧ���ҳ������ʾ����飬�����ʾ�140�ݣ�ÿλѧ���ļҳ�1�ݣ�ÿ���ʾ�������һ��̬�ȣ������յ��ʾ�����������������յ��ʾ�����Ч����������������������������ͳ��ͼ��
ѧ���ҳ��Ժ���ʹ���ֻ���̬�����ͳ��ͼ
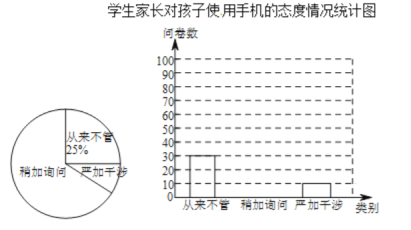
����������Ϣ�ش��������⣺
��1�����յ��ʾ���Ϊ �ݣ����ϼӸ��������ֶ�Ӧ���ε�Բ�ĽǶ���Ϊ ��
��2��������ͳ��ͼ����������
��3���������Լ�ѯ��������������������Ϊ����������������֪ȫУ��1500��ѧ��������Ƹ�У�Ժ���ʹ���ֻ��������������ļҳ���Լ�ж����ˣ�
���𰸡���1��120��30������2���𰸼���������3��1375�ˣ�
��������
��1�������������������������Ͱٷֱ�����ܷ����������ܷ������ϼӸ���ķ�������ٷֱȣ�Ȼ�����Բ�ĽǵĶ�����
��2�������ܷ�������Լ�ѯ�ʵ�������Ȼ��ȫͳ��ͼ��
��3������������������������������Լ�ѯ�����İٷֱ����ȫУ��������
�⣺��1��30��25%=120���ˣ�
10��120��360��=30��
�ʴ�Ϊ��120��30��
��2����ͼ��ʾ��

��3��1500��![]() =1375���ˣ�
=1375���ˣ�
����Ƹ�У�Ժ���ʹ���ֻ��������������ļҳ���Լ��1375�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У� ![]() ��ֱ��
��ֱ��![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ����
����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ����
����![]() ���߶�
���߶�![]() ��ʱ����ͼ�٣���֤��
��ʱ����ͼ�٣���֤��![]() ��
��
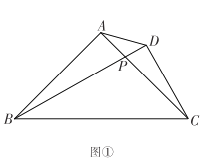
![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ƶ�ʱ��λ����ͼ�ڡ�ͼ����ʾ���߶�
���ƶ�ʱ��λ����ͼ�ڡ�ͼ����ʾ���߶�![]() ��
��![]() ֮������������������ϵ����ֱ��д����IJ��룬����֤����
֮������������������ϵ����ֱ��д����IJ��룬����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�� 3 ����ȫ��ѧ�� 2019 ����б�ҵ�������Եijɼ�ͳ�����±���
�ɼ� | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
���� | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
�����ϱ��е���Ϣ�жϣ����н����д������ �� ��
A.�ð�һ���� 40 ��ͬѧB.�ð�ѧ����ο��Գɼ��������� 45 ��
C.�ð�ѧ����ο��Գɼ�����λ���� 44 ��D.�ð�ѧ����ο��Գɼ���ƽ������ 45 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������BCE�У���A�DZ�BE��һ�㣬��ABΪֱ���ġ�O��CE�����ڵ�D��AD��OC����FΪOC���O�Ľ��㣬����AF.
��1����֤��CB�ǡ�O�����ߣ�
��2������ECB=60����AB=6����ͼ����Ӱ���ֵ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У���P��AC���ϵ�һ�㣬����P����BCƽ�е�ֱ��PQ����AB�ڵ�Q����D���߶� BC�ϣ�����AD���߶�PQ�ڵ�E����![]() ����G��BC�ӳ����ϣ���ACG��ƽ���߽�ֱ��PQ�ڵ�F��
����G��BC�ӳ����ϣ���ACG��ƽ���߽�ֱ��PQ�ڵ�F��
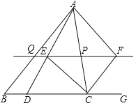
��1����֤��PC��PE��
��2����P�DZ�AC���е�ʱ����֤���ı���AECF�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ���A(-1,0)��B��4,5����������![]() +b
+b![]() +c����A��B����
+c����A��B����
��1���������ߵĽ���ʽ��
��2����M���߶�AB�ϵ�һ�㣨����A��B�غϣ�����M��![]() ��Ĵ��߽����������N�����߶�MN�����ֵ���������M��N�����ꣻ
��Ĵ��߽����������N�����߶�MN�����ֵ���������M��N�����ꣻ
��3���ڣ�2���������£������������Ƿ���ڵ�P��ʹ�èSPMN����MNΪֱ�DZߵ�ֱ�������Σ������������P�����꣬����������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABΪ��O��ֱ������CΪ��AB���е㣬��DΪ��O��һ�㣬����CD����AB�ڵ�M��AEΪ��DAM��ƽ���ߣ���CD�ڵ�E��
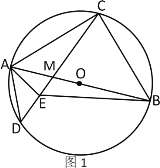
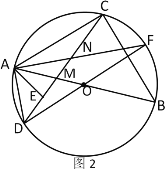
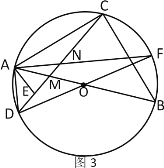
��1����ͼ1������BE������ACD=22�������MBE�Ķ�����
��2�� ��ͼ2������DO���ӳ�������O�ڵ�F������AF����CD�ڵ�N��
����֤��DM2+CN2=CM2��
����ͼ3����AD=1��AB=![]() ʱ����ֱ��д���߶�ME�ij���
ʱ����ֱ��д���߶�ME�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������y��ax2��2x+c(a��0)��x�ύ��A��B����(A����B�����)����y�ύ�ڵ�C(0����3)���Գ�����ֱ��x��1����ACB�����ԲM��y������������D������AD��CM�����ӳ�CM��x���ڵ�E��
(1)�������ߵĺ�������ʽ��ֱ��BC�ĺ�������ʽ��
(2)��֤����CAD�ס�CEB��
(3)��ͼ2��PΪx���������ϵ�һ�����㣬OP��t��(0��t��3)����P����y��ƽ�е�ֱ�߽����������Q������QAD�����ΪS��д��S��t�ĺ�������ʽ���ʣ���tΪ��ֵʱ����QAD����������������Ϊ���٣�
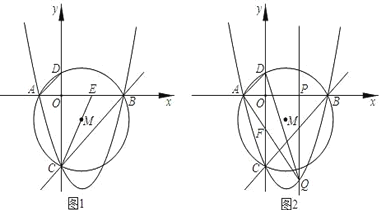
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+2x+c��x�ύ��A����1��0��B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1���������ߵĽ���ʽ��ֱ��AC�Ľ���ʽ��
��2������y������һ��M��ʹ��BDM���ܳ���С�������M�����ꣻ
��3����̽�����ڒ��������Ƿ���ڵ�P��ʹ�Ե�A��P��CΪ���㣬ACΪֱ�DZߵ���������ֱ�������Σ������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com