
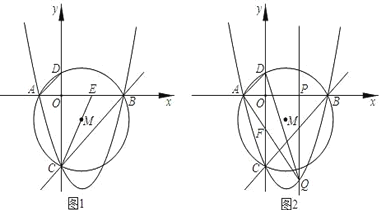
【题目】如图1,已知抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,△ACB的外接圆M交y轴的正半轴与点D,连结AD、CM,并延长CM交x轴于点E.
(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)求证:△CAD∽△CEB;
(3)如图2,P为x轴正半轴上的一个动点,OP=t,(0<t<3),过P点与y轴平行的直线交抛物线与点Q,若△QAD的面积为S,写出S与t的函数表达式,问:当t为何值时,△QAD的面积最大,且最大面积为多少?
【答案】(1)![]() ,BC:
,BC:![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]() 时,
时,![]() .
.
【解析】
(1)先根据图像得到a,c的值,进而可得到A、B两点的坐标,再求出函数解析式即可;(2)如图,连结AM,根据同弧所对的圆周角相等得到∠ADC=∠ABC=45°,根据圆周角定理可得∠AMC=90°,进而得到∠ACE=45°,所以∠ACD =∠ECB=45°-∠ECD,即可证明△ACD∽△ECB;(3)根据题意易得△AOF∽△APQ,再根据对应边成比例得到OF与PQ的关系,将Q点横坐标代入抛物线方程求出PQ的长度,进而求出OF的长度,再根据S=S△ADF+S△QDF求出S与t的函数表达式,再求出最大值即可.
解:(1)∵抛物线的对称轴是x=1,
∴![]() =1,∴a=1
=1,∴a=1
由图像易知c=-3,所以抛物线解析式为![]() , B(3,0),A(-1,0),C(0,-3)
, B(3,0),A(-1,0),C(0,-3)
设直线BC的函数表达式为:y=kx+b,
则![]() ,解得:k=1,b=-3,
,解得:k=1,b=-3,
∴直线BC的解析式为![]() ;
;
(2)如图,连结AM,
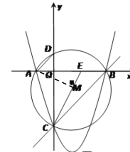
∵OB=OC,∴∠OCB=∠OBC=45°,
∴∠ADC =∠OBC=45°,∠AMC=90°,
又∵AM=CM,∴∠ACE=45°,
∴∠ACD =∠ECB=45°-∠ECD,
∴△ACD∽△ECB
(3)∵PQ∥y轴,∴△AOF∽△APQ,
∴![]() .
.
∴![]() ,
,
∵PQ=![]() ,∴
,∴![]() ,
,
∴S=S△ADF+S△QDF=![]()
![]()
整理得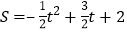 ,
,
化为顶点式得S=﹣![]() (t-
(t-![]() )2+
)2+![]() ,∴当
,∴当![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线![]() 经过点
经过点![]() ,记双曲线与两坐标轴之间的部分为
,记双曲线与两坐标轴之间的部分为![]() (不含双曲线与坐标轴).
(不含双曲线与坐标轴).
(1)求![]() 的值;
的值;
(2)求![]() 内整点的个数;
内整点的个数;
(3)设点![]() 在直线
在直线![]() 上,过点
上,过点![]() 分别作平行于
分别作平行于![]() 轴
轴![]() 轴的直线,交双曲线
轴的直线,交双曲线![]()
![]() 于点
于点![]() ,记线段
,记线段![]() 、双曲线所围成的区域为
、双曲线所围成的区域为![]() ,若
,若![]() 内部(不包括边界)不超过
内部(不包括边界)不超过![]() 个整点,求
个整点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.
学生家长对孩子使用手机的态度情况统计图
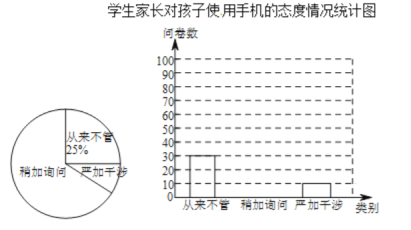
根据以上信息回答下列问题:
(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 ;
(2)把条形统计图补充完整;
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
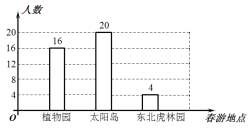
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学现有学生2 870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
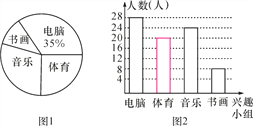
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将小易画的统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计实验中学现有的学生中,有多少人爱好“书画”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九年级学生的体能状况,从我校九年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A,B,C,D四个等级,请根据两幅图中的信息回答下列问题:
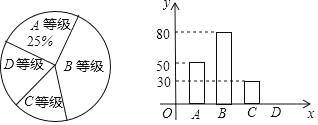
(1)求本次测试共调查了 名学生,补全条形统计图;
(2)B等级人数对应扇形统计图的圆心角的大小为 ;
(3)我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为C等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,以下结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),(1.5,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
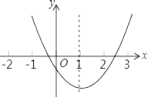
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
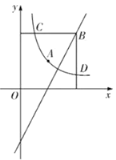
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
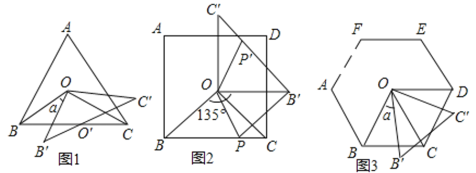
【题目】在下列正多边形中,![]() 是中心,定义:
是中心,定义:![]() 为相应正多边形的基本三角形.如图1,
为相应正多边形的基本三角形.如图1,![]() 是正三角形
是正三角形![]() 的基本三角形;如图2,
的基本三角形;如图2,![]() 是正方形
是正方形![]() 的基本三角形;如图3,
的基本三角形;如图3,![]() 为正
为正![]() 边形
边形![]() …的基本三角形.将基本
…的基本三角形.将基本![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角度得
角度得![]() .
.
(1)若线段![]() 与线段
与线段![]() 相交点
相交点![]() ,则:
,则:
图1中![]() 的取值范围是________;
的取值范围是________;
图3中![]() 的取值范围是________;
的取值范围是________;
(2)在图1中,求证![]()
(3)在图2中,正方形边长为4,![]() ,边
,边![]() 上的一点
上的一点![]() 旋转后的对应点为
旋转后的对应点为![]() ,若
,若![]() 有最小值时,求出该最小值及此时
有最小值时,求出该最小值及此时![]() 的长度;
的长度;
(4)如图3,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com