
【题目】已知:AB为⊙O的直径,点C为弧AB的中点,点D为⊙O上一点,连接CD,交AB于点M,AE为∠DAM的平分线,交CD于点E.
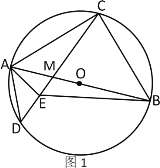
(1)如图1,连接BE,若∠ACD=22°,求∠MBE的度数;
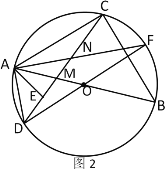
(2) 如图2,连接DO并延长,交⊙O于点F,连接AF,交CD于点N.
①求证:DM2+CN2=CM2;
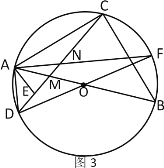
②如图3,当AD=1,AB=![]() 时,请直接写出线段ME的长.
时,请直接写出线段ME的长.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]()
【解析】
(1)由圆周角定理,得到∠CAB=∠ABC=∠ADC= 45°,由角平分线的定义和三角形的外角性质,得到∠CAE=∠CEA,结合等腰三角形的性质和三角形的内角和定理,即可求出答案;
(2)①根据题意,将△ADM绕点A逆时针旋转90°,得到![]() ,连接
,连接![]() ,由旋转的性质,△ADM≌△
,由旋转的性质,△ADM≌△![]() ,得到DM=
,得到DM=![]() ,然后证明△
,然后证明△![]() AC≌△MAC,得到
AC≌△MAC,得到![]() =CM,利用勾股定理,即可得到结论成立;
=CM,利用勾股定理,即可得到结论成立;
②连接CF,由(1)可知AC=BC=CE,根据等腰直角三角形的性质和勾股定理求出CE的长度,然后利用相似三角形的判定和性质,得到线段的比,然后构建方程,求出CM的长度,即可得到ME的长度.
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵点C为弧AB中点,
∴![]() =
=![]() ,
,
∴∠CAB=∠ABC=∠ADC= 45°,AC=BC
∴△ACB是等腰直角三角形
∵![]() ∠DAM的平分线,
∠DAM的平分线,
∴∠MAE=∠EAD
∵∠CAE=∠CAB+∠MAE,∠CEA=∠ADC+∠EAD,
∴∠CAE=∠CEA,
∴AC=CE=BC
∴∠CBE=∠CBM+∠MBE=![]()
∵∠ACD=22°,
![]()
又∵∠CBM=45°
∴∠MBE=![]() ;
;
(2)证明:将△ADM绕点A逆时针旋转90°,得到![]() ,连接
,连接![]() ,
,
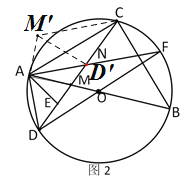
∵DF是⊙O的直径,
∴∠DAF=90°
∵∠ADC=45°
∴△AND为等腰三角形,AD=AN
∴![]() 和AN重合
和AN重合
∴△ADM≌△ANM’
∴DM=![]() ,AM=
,AM=![]() ,∠
,∠![]() =∠ADC=45°,
=∠ADC=45°,
∵∠M’ AM=90°,∠CAB=45°,
∴∠![]() =45°
=45°
∴△M’ AC≌△MAC(SAS),
∴![]() =CM
=CM
∵∠M’NA=∠ADC=∠AND=45°,
∴∠M’ND=∠M’NC=90°,
∴M’ N2+ CN 2=C M’ 2,
∴MD2+ CN 2=C M2 ;
(3)如图:连接CF,
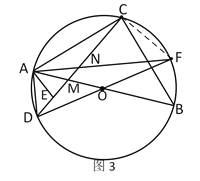
∵AB与DF为直径,AB=![]() ,AD=1,
,AD=1,
∴∠DCF=90°,∠DAF=90°,
∴![]() ,
,
由(1)可知,△AND是等腰直角三角形,△ABC是等腰直角三角形,
∴AN=AD=1,∠AND=45°,AC=BC=CE=![]() ,
,
∴NF=3-1=2,
∴△CNF是等腰直角三角形,
∴CN=CF=![]() ,
,
∴![]() ,
,
∵∠AMD=∠CMB,∠ADM=∠CBM=45°,
∴△ADM∽△CBM,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
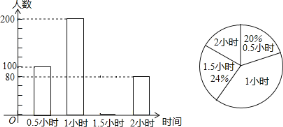
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
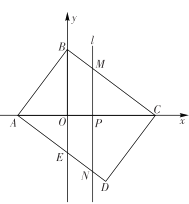
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 动点
动点![]() 从原点出发,以每秒 1 个单位长度的速度沿
从原点出发,以每秒 1 个单位长度的速度沿![]() 轴正方向移动,移动时间为
轴正方向移动,移动时间为![]() 秒,过点 P 作垂直于
秒,过点 P 作垂直于![]() 轴的直线
轴的直线![]() ,交
,交![]() 于点 M ,交
于点 M ,交![]() 或
或![]() 于点 N ,直线
于点 N ,直线![]() 扫过矩形
扫过矩形![]() 的面积为
的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 移动过程中到点
移动过程中到点![]() 之前的
之前的![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在直线![]() 移动过程中,第一象限的直线
移动过程中,第一象限的直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰直角三角形? 若存在,直接写出点
是等腰直角三角形? 若存在,直接写出点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.
学生家长对孩子使用手机的态度情况统计图
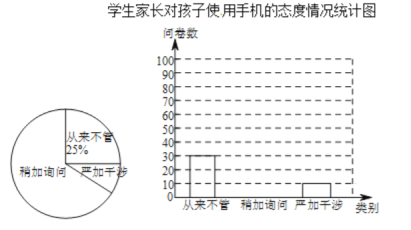
根据以上信息回答下列问题:
(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 ;
(2)把条形统计图补充完整;
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
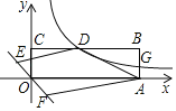
【题目】如图,反比例函数y=![]() (x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
(x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
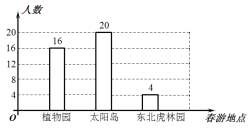
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学现有学生2 870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
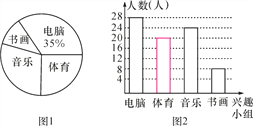
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将小易画的统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计实验中学现有的学生中,有多少人爱好“书画”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,以下结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),(1.5,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
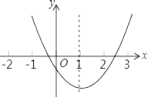
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东方向上的B处,这时轮船B与小岛A的距离是( )
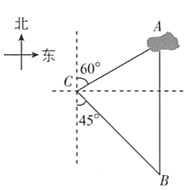
A.![]() 海里B.
海里B.![]() 海里C.120海里D.60海里
海里C.120海里D.60海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com