
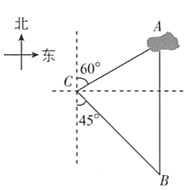
【题目】如图,一艘轮船从位于灯塔C的北偏东方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东方向上的B处,这时轮船B与小岛A的距离是( )
A.![]() 海里B.
海里B.![]() 海里C.120海里D.60海里
海里C.120海里D.60海里
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,点C为弧AB的中点,点D为⊙O上一点,连接CD,交AB于点M,AE为∠DAM的平分线,交CD于点E.
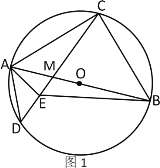
(1)如图1,连接BE,若∠ACD=22°,求∠MBE的度数;
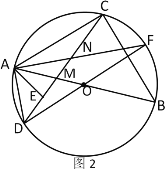
(2) 如图2,连接DO并延长,交⊙O于点F,连接AF,交CD于点N.
①求证:DM2+CN2=CM2;
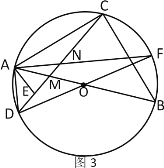
②如图3,当AD=1,AB=![]() 时,请直接写出线段ME的长.
时,请直接写出线段ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)经过点(﹣1,0),且满足4a+2b+c>0,有下列结论:①a+b>0;②﹣a+b+c>0;③b2﹣2ac>5a2.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在开业前,所进三种货物:上衣、裤子和鞋子的数量共480份,这三种货物进货的数量比例如图(1)所示.商店安排6人只销售上衣,4人只销售裤子,2人只销售鞋子,用了5天的时间销售货物的情况如图(2)及表格所示.
(1)求所进三种货物中上衣有多少件?
(2)直接在图中把图(2)补充完整;
(3)表格中的![]() = (直接填空);
= (直接填空);
(4)若销售人员不变,并以同样的销售速度销售,则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

货物 | 上衣(件) | 裤子(条) | 鞋子(双) |
5天的销售总额 | 150 | a | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以3元/本的价格购进某种笔记本若干,然后以5元/本的价格出售,每天售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若每本降价![]() 元,则每天的销售量是________本(用含
元,则每天的销售量是________本(用含![]() 的代数式表示).
的代数式表示).
(2)要想每天赢利60元,该超市需将每本的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
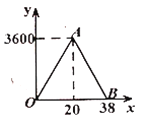
【题目】某校学生食堂共有座位![]() 个,某天午餐时,食堂中学生人数
个,某天午餐时,食堂中学生人数![]() (人)与时间
(人)与时间![]() (分钟)
(分钟)
变化的函数关系图象如图中的折线![]() .
.
(1)试分别求出当![]() 与
与![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该校学生数有![]() 人,考虑到安全因素,学校决定对剩余
人,考虑到安全因素,学校决定对剩余![]() 名同学延时用餐,即等食堂空闲座位不少于
名同学延时用餐,即等食堂空闲座位不少于![]() 个时,再通知剩余
个时,再通知剩余![]() 名同学用餐.请结合图象分析,这
名同学用餐.请结合图象分析,这![]() 名学生至少要延时多少分钟?
名学生至少要延时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数![]() 图像交
图像交![]() 轴于
轴于![]() ,交
,交![]() 交轴于点
交轴于点![]() ,
,![]() 是抛物线的顶点,对称轴
是抛物线的顶点,对称轴![]() 经过
经过![]() 轴上的点
轴上的点![]() .
.
(1)求二次函数关系式;
(2)对称轴![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为对称轴
为对称轴![]() 上一动点.
上一动点.
①求![]() 的最小值及取得最小值时点
的最小值及取得最小值时点![]() 的坐标;
的坐标;
②在①的条件下,把![]() 沿着
沿着![]() 轴向右平移
轴向右平移![]() 个单位长度
个单位长度![]() 时,设
时,设![]() 与
与![]() 重叠部分面积记为
重叠部分面积记为![]() ,求
,求![]() 与
与![]() 之间的函数表达式,并求出
之间的函数表达式,并求出![]() 的最大值.
的最大值.
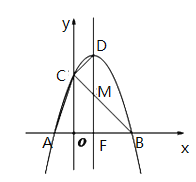
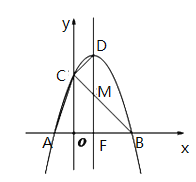
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com