
分析 整式方程:方程里所有的未知数都出现在分子上,分母只是常数而没有未知数.
一元二次方程:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程.
解答 解:①2x2-3=0;③$\frac{1}{2}$y-$\frac{1}{3}$y2+1=0;④ay2+2y+c=0;⑤y-x2=0;⑥(x+1)(x-3)=x2+5,中的未知数都出现在分子上,分母只是常数而没有未知数,属于整式方程.
①2x2-3=0、③$\frac{1}{2}$y-$\frac{1}{3}$y2+1=0符合一元二次方程的定义,属于一元二次方程;
当a=0时,方程ay2+2y+c=0属于一元一次方程;
⑤y-x2=0中含有2个未知数,属于二元二次方程;
⑥由(x+1)(x-3)=x2+5得到:-2x-8=0,未知数x的最高次数是1,属于一元一次方程.
故答案是:①③④⑤⑥;①③.
点评 本题考查了一元二次方程的定义.一元二次方程必须同时满足三个条件:
①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数;
②只含有一个未知数;
③未知数的最高次数是2.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
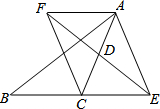 已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.
已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com