
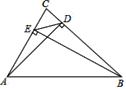
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的高.求证:
边上的高.求证:![]() .
.
【答案】见解析
【解析】
要证明![]() ,这两个三角形已经有一个公共角相等,此时可以考虑用两组对应边的比相等且相应的夹角相等的两个三角形相似,即找到CD:CA与CE:CB是否相等,这时不能直接的找出,则充分利用题干“
,这两个三角形已经有一个公共角相等,此时可以考虑用两组对应边的比相等且相应的夹角相等的两个三角形相似,即找到CD:CA与CE:CB是否相等,这时不能直接的找出,则充分利用题干“![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的高”中的垂直关系找到角相等的关系,再证明△CDA∽△CEB得到CD:CE=CA:CB从而运用比例的基本性质得到CD:CA=CE:CB.
边上的高”中的垂直关系找到角相等的关系,再证明△CDA∽△CEB得到CD:CE=CA:CB从而运用比例的基本性质得到CD:CA=CE:CB.
证明:∵在△ABC中,AD、BE分别是BC、AC边上的高
∴∠ADC=∠BEC=90°
∵∠C是公共角,∴△CDA∽△CEB(两组角对应相等的两个三角形相似)
∴CD:CE=CA:CB(相似三角形对应边成比例)
∴CD:CA=CE:CB(比例的基本性质)
∴△DCE∽△ACB.(两组对应边的比相等且相应的夹角相等的两个三角形相似)


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
(1)求直线![]() 的表达式;
的表达式;
(2)过点A做平行于x轴的直线l,l与抛物线![]() (a>0)交于B,C两点。若BC≥4,求a的取值范围;
(a>0)交于B,C两点。若BC≥4,求a的取值范围;
(3)设直线![]() 与抛物线
与抛物线![]() 交于D,E两点,当3
交于D,E两点,当3![]() ≤DE≤5
≤DE≤5![]() 时,结合函数的图象,直接写出m的取值范围是____________________。
时,结合函数的图象,直接写出m的取值范围是____________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
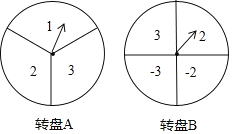
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
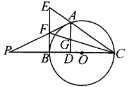
(1)求证:BF=EF;
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD和FG的长度.
,求BD和FG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
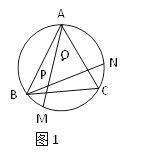
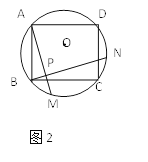
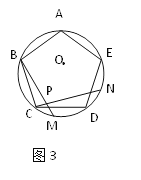

(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣1,1),B(﹣4,1),C(﹣3,3).
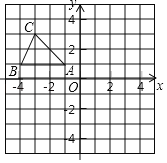
(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;并判断以O,A1,B为顶点的三角形的形状(直接写出结果);
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2,并求出点C旋转到C2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,《九章算术》是我国古代数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是________步.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com