
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.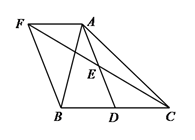
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
【答案】
(1)
证明:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD
(2)
解:当△ABC满足AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴□AFBD是矩形
【解析】根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;
(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】若(x+y)3-xy(x+y)=(x+y)·M(x+y≠0),则M是( )
A. x2+y2 B. x2-xy+y2 C. x2-3xy+y2 D. x2+xy+y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.求:m
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为( )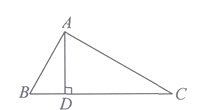
①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB;
④点A到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离;
⑥AD+BD>AB.
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A.掷一枚硬币,正面朝上
B.a是实数,|a|≥0
C.某运动员跳高的最好成绩是20.1米
D.从车间刚生产的产品中任意抽取一个,是次品
查看答案和解析>>
科目:初中数学 来源: 题型:
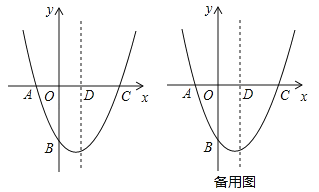
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象经过点A(﹣1,0),B(0,
的图象经过点A(﹣1,0),B(0,![]() ),C(2,0),其对称轴与x轴交于点D.
),C(2,0),其对称轴与x轴交于点D.
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则![]() PB+PD的最小值为 ;
PB+PD的最小值为 ;
(3)M(x,t)为抛物线对称轴上一动点.
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com