练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知⊙O的直径是4cm，OP＝4cm，则点P（　　）

    A.在⊙O外B.在⊙O上C.在⊙O内D.不能确定

    【答案】A

    【解析】

    根据点到圆心的距离和圆的半径之间的数量关系，即可判断点和圆的位置关系．点到圆心的距离小于圆的半径，则点在圆内；点到圆心的距离等于圆的半径，则点在圆上；点到圆心的距离大于圆的半径，则点在圆外．

    解：∵点到圆心的距离d＝4＞2＝r，

    ∴该点P在⊙O外．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝x2﹣6x+1，关于该函数在﹣1≤x≤4的取值范围内，下列说法正确的是（　　）

    A.有最大值8，最小值﹣8B.有最大值8，最小值﹣7

    C.有最大值﹣7，最小值﹣8D.有最大值1，最小值﹣7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校校长寒假将带领该校市级三好学生去旅游。甲旅行社说：“若校长买全票一张，则其学生可享受半价优惠。”乙旅行社说：“包括校长在内全部按全票的6折优惠”。若全票价为240元，则：
    （1）设学生数为 ，分别计算两家旅行社的收费（用含 的式子表示）；
    （2）如何选择两家旅行社，可使学校更划算。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个单项式加上多项式9（x﹣1）2﹣2x﹣5后等于一个整式的平方，试求所有这样的单项式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】-278×1=（ ）
    A.0
    B.278
    C.1
    D.-278

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．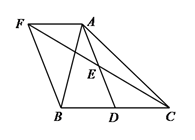

    （1）求证：BD=CD；
    （2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）(-4)×3+(-18)÷(-2)
    （2）
    （3）先化简，再求值：x2一(5x2—4y)+3(x2一y)其中x=一1，y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常烦琐，且易出错．聪明的小高斯经过探索后，给出了下面漂亮的解答过程．
    解：设S=1+2+3+…+100， ①
    则S=100+99+98+…+1，②
    ①+②，得
    2S=101+101+101+…+101．
    (两式左右两端分别相加，左端等于2s，右端等于100个101的和)
    所以2S=100x101，
    S= ×100X101=5050 ③
    所以1+2+3+…+100=5050．
    后来人们将小高斯的这种解答方法概括为“倒序相加法”．
    请解答下面的问题：
    （1）请你运用高斯的“倒序相加法”计算：1+2+3+…+200．
    （2）请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式，猜想：
    1+2+3+…+n= ．
    （3）计算：101+102+103+…+2018．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如下图。

    （1）观察发现：如图1，已知Rt△ABC，∠ABC=90°，分别以AB，BC为边，向外作正方形ABDE和正方形BCFG，连接DG．若M是DG的中点，不难发现：BM= AC．
    请完善下面证明思路：①先根据 ，证明BM= DG；②再证明 ，得到DG=AC；所以BM= AC；
    （2）数学思考：若将上题的条件改为：“已知Rt△ABC，∠ABC=90°，分别以AB，AC为边向外作正方形ABDE和正方形ACHI，N是EI的中点”，则相应的结论“AN= BC”成立吗？小颖通过添加如图2所示的辅助线验证了结论的正确性．请写出小颖所添加的辅助线的作法，并由此证明该结论；
    （3）拓展延伸：如图3，已知等腰△ABC和等腰△ADE，AB=AC，AD=AE．连接BE，CD，若P是CD的中点，探索：当∠BAC与∠DAE满足什么条件时，AP= BE，并简要说明证明思路．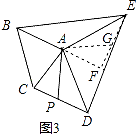

    查看答案和解析>>

    同步练习册答案