
 如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=32°,则∠BOF=122°.
如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=32°,则∠BOF=122°. 科目:初中数学 来源: 题型:解答题
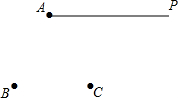 如图,平面上有射线AP和点B、点C,按下列语句要求画图:
如图,平面上有射线AP和点B、点C,按下列语句要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com