Question

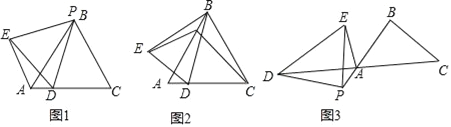
【题目】已知：等边△ABC的边长为4，点P在线段AB上，点D在线段AC上，且△PDE为等边三角形，当点P与点B重合时（如图1），AD+AE的值为　 　；

[类比探究]在上面的问题中，如果把点P沿BA方向移动，使PB=1，其余条件不变（如图2），AD+AE的值是多少？请写出你的计算过程；

[拓展迁移]如图3，△ABC中，AB=BC，∠ABC=a，点P在线段BA延长线上，点D在线段CA延长线上，在△PDE中，PD=PE，∠DPE=a，设AP=m，则线段AD、AE有怎样的等量关系？请用含m，a的式子直接写出你的结论．

Answer 1

【答案】（1）4．（2）[类比探究]： AD+AE=3（3）[拓展迁移]： AD﹣AE=2msin．

【解析】试题分析：（1）只要证明△EPA≌△DPC，即可推出AE=CD，可得AD+AE=AD+DC=AC=4；

（2）[类比探究]：如图2中，作PK∥BC交AC于K．连接AE．利用（1）中的结论即可解决问题；

（3）[拓展迁移]：如图3中，作PJ⊥AD于J，在AD上取一点K，使得PK=PA．由△PDK≌△PEA，推出DK=AE，推出AD﹣AE=AK=2AJ=2msin即可解决问题；

试题解析：（1）如图1中，

∵△PDE．△PAC都是等边三角形，∴PE=PD，PA=PC，∠EPD=∠APC=60°，

∴∠EPA=∠DPC，∴△EPA≌△DPC，∴AE=CD，∴AD+AE=AD+DC=AC=4．

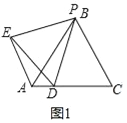
（2）[类比探究]： AD+AE=3

理由：如图2中，作PK∥BC交AC于K．连接AE．

易证△PAK是等边三角形，

由上面题目可知．AE+AD=AK=3．

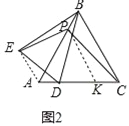
（3）[拓展迁移]：如图3中，作PJ⊥AD于J，在AD上取一点K，使得PK=PA．

易证∠APK=∠DPE=α，

∵PD=PE，PK=PA，∴∠DPK=∠EPA，∴△PDK≌△PEA，∴DK=AE，

∴AD﹣AE=AK=2AJ=2msin．∴AD﹣AE=2msin．