
【题目】某地区有城区居民和农村居民共80万人,某机构准备采用抽取样本的方法调查该地区居民“获取信息的最主要途径”.
⑴该机构设计了以下三种调查方案:
方案一:随机抽取部分城区居民进行调查;
方案二:随机抽取部分农村居民进行调查;
方案三:随机抽取部分城区居民和部分农村居民进行调查.
其中最具有代表性的一个方案是________;
⑵该机构采用了最具有代表性的调查方案进行调查.供选择的选项有:电脑、手机、电视、广播,其他,共五个选项,每位被调查居民只选择一个选项.现根据调查结果绘制如下统计图,请根据统计图回答下列问题:

①这次接受调查的居民人数为________人;
②统计图中人数最多的选项为________;
③请你估计该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数.
【答案】(1)方案三;(2)①1000;②手机;③52.8万人.
【解析】
(1)根据三个方案选出最具有代表性的一个方案即可;
(2)①把电脑、手机、电视、广播、其他,这五个选项的总人数相加即可;
②从统计图中找出人数最多的选项即可;
③用80×该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的人数所占的百分比即可得到结论.
解:(1)最具有代表性的一个方案是方案三,
故答案为:方案三;
(2)①这次接受调查的居民人数为260+400+150+100+90=1000人;
②统计图中人数最多的选项为手机;
③![]() 万人,
万人,
答:该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数52.8万人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以![]() 的直角边
的直角边![]() 为直径的
为直径的![]() 交斜边
交斜边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线与
的切线与![]() 交于点
交于点![]() ,弦
,弦![]() 与
与![]() 垂直,垂足为
垂直,垂足为![]() .
.
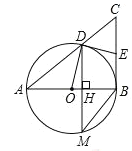
![]() 求证:
求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 的面积为
的面积为![]() ,两个三角形
,两个三角形![]() 和
和![]() 的外接圆面积之比为
的外接圆面积之比为![]() ,求
,求![]() 的内切圆面积
的内切圆面积![]() 和四边形
和四边形![]() 的外接圆面积
的外接圆面积![]() 的比.
的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
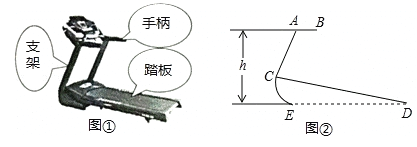
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
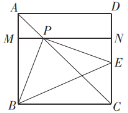
【题目】如图,P是边长为1的正方形ABCD的对角线AC上一动点(不与A、C两点重合),连接BP,过点P作PE⊥PB交直线CD于点E,连接BE,MN//BC分别交AB、DC于点M、N.设![]() .
.
(1)当点E在CD边上时,线段PE于线段PB有怎样的数量关系?试证明你的结论.
(2)设以点B,C,P,E为顶点的四边形的面积为y,试确定y与x之间的函数关系式,并求出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种健身产品在市场上很受欢迎,该公司每年的年产量为6万件,每年可在国内和国外两个市场全部销售,若在国内销售,平均每件产品的利润y1(元)与国内销售量x(万件)的函数关系式为![]() ,若在国外销售,平均每件产品的利润为71元.
,若在国外销售,平均每件产品的利润为71元.
(1)求该公司每年的国内和国外销售的总利润w(万元)与国内销售量x(万件)的函数关系式,并指出x的取值范围.
(2)该公司每年的国内国外销售量各为多少时,可使公司每年的总利润最大?最大值是多少?
(3)该公司计划在国外销售不低于5万件,并从国内销售的每件产品中捐出2m(5≤m≤10)元给希望工程,从国外销售的每件产品中捐出m元给希望工程,若这时国内国外销售的最大总利润为393万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛,需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知毎袋贴纸有50张,毎袋小红旗有20面,贴纸和小红旗需整袋购买,每袋贴纸价格比每袋小红旗价格少5元,用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果给每位演出学生分发国旗图案贴纸2张,小红旗1面.设购买国旗图案贴纸![]() 袋(
袋(![]() 为正整数),则购买小红旗多少袋能恰好配套?请用含
为正整数),则购买小红旗多少袋能恰好配套?请用含![]() 的代数式表示.
的代数式表示.
(3)在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数![]() 的图象绕点
的图象绕点![]() 旋转
旋转![]() ,得到新函数
,得到新函数![]() 的图象,我们称
的图象,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图象的对称轴与
的图象的对称轴与![]() 轴交点坐标为
轴交点坐标为![]() .
.
(1)填空:![]() 的值为 (用含
的值为 (用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)当![]() 时,
时,![]() 的图象与
的图象与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧).与
的右侧).与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 原点
原点![]() 逆时针旋转
逆时针旋转![]() ,得到它的对应线段
,得到它的对应线段![]() ,若线
,若线![]() 与
与![]() 的图象有公共点,结合函数图象,求
的图象有公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值:
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com