Question

11．甲、乙两车在相距300千米的A、B两地匀速相向而行，两车同时出发，途中甲车配货停留1小时．甲、乙两车离B地的距离y（千米）与出发时间x（小时）之间的关系如图①所示，甲、乙两车间的距离s（千米）与出发时间x（小时）之间的关系如图②所示，
（1）求甲、乙两车的速度；
（2）求甲车到B地所用的时间，并将图②补充完整；
（3）乙出发多少小时时，两车相距20千米？

Answer 1

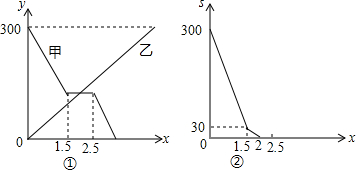
分析 （1）结合图①图②可知，当1.5≤x≤2.5时，甲车在装货，结合图②中点的坐标即可求出甲、乙两车的速度；
（2）由时间=路程÷速度+停留时间，即可得出甲车到达的时间，结合一次函数的性质，可补充完整图②；
（3）由图②中点的意义可得知两车两次相距20千米时，甲车都在装货，由时间=路程÷速度即可得出结论．

解答 解：（1）结合图形①②可知：乙车的速度为30÷（2-1.5）=60（千米/小时）；
甲车的速度为（300-30）÷1.5-60=120（千米/小时）．
答：甲车的速度为120千米/小时，乙车的速度为60千米/小时．
（2）甲车到乙地的时间为300÷120+1=3.5（小时）．
答：甲车到B地所用的时间为3.5小时．
补充完图②如下图所示．
 
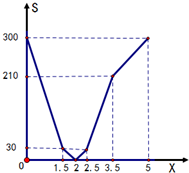
（3）由图形②可知，当两车相距20千米时，甲车正在装货．
当两车第一次相距20千米时，乙车出发时间为：1.5+（30-20）÷60=$\frac{5}{3}$（小时）；
当两车第二次相距20千米时，乙车出发时间为：1.5+（30+20）÷60=$\frac{7}{3}$（小时）．
答：乙出发$\frac{5}{3}$或$\frac{7}{3}$小时时，两车相距20千米．

点评 本题考查了一次函数的意义，解题的关键是：（1）结合函数图象，求出速度；（2）时间=路程÷速度+停留时间；（3）分析出两车相距20千米时两车的运动状态．本题属于中档题，（1）（2）难度不大，（3）有点难度，需要考虑到两车相距20千米时，两车的运动状况．