
【题目】从一副扑克牌中的13张黑桃牌中随机抽取一张,它是王牌的概率为____.
 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】用长为32米的篱笆围成一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.
(1)求y关于x的函数关系式;
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积最大的养鸡场?如果能,请求出其边长及最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由. 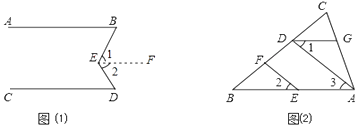
(1)完成正确的证明:如图(1),已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1=()
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2=()
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
(2)如图(2),在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.()
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥()
所以∠BAC+=180° ().
又因为∠BAC=70°,所以∠AGD=110°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=4cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒后⊙P与直线CD相切.
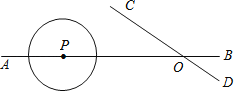
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.据此规律计算:每件商品降价元时,商场日盈利可达到2100元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , ![]() = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
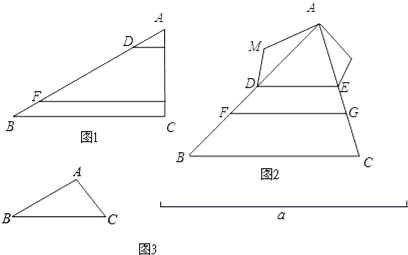
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com