
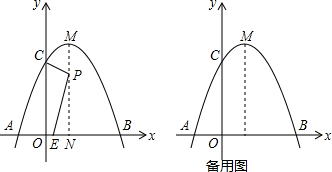
分析 (1)将解析式配成顶点式即可.
(2)当点E与O重合时,设PN=m,过点C作CF⊥MN于F,由△ENP∽△PFC用相似比例建立方程解之即可.
(3)找到左右两个极端位置即可.P在M点时,E在右边最运处,这个时候求出EN为对称轴右边的路径长度;E点在左侧时,设EN=y,PN=x,由△ENP∽△PFC列出比例方程,得到y关于x的二次函数,配方求出最大值,再加上右边路径长度即为总路径长度.
解答 解:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴M(1,4);
(2)当点E与O重合时,EN=1,设PN=m,
过点C作CF⊥MN,垂足为F,如图1,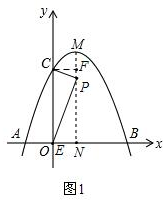
∵∠EPC=90°,
∴∠EPN+∠NEP=∠EPN+∠CPF=90°,
∴∠CPF=∠PEN,
∴△ENP∽△PFC
∴$\frac{CF}{PF}=\frac{PN}{EN}$,即:$\frac{1}{3-m}=\frac{m}{1}$,
解得:m=$\frac{3±\sqrt{5}}{2}$
∴点P的坐标为:(1,$\frac{3+\sqrt{5}}{2}$)或(1,$\frac{3-\sqrt{5}}{2}$)
(3)①当点P与M重合时,如图2,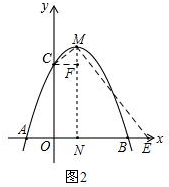
由△ENM∽△MFC可知,$\frac{EN}{MN}=\frac{MF}{CF}$,
∴EN=4,
即当点P从M运动到F时,点E运动的路径长EN为4;
②当点P从F运动到N时,点E从点N向左运动到某最远点后,回到点N结束.如图3,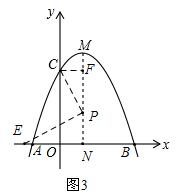
设EN=y,PN=x,
由△ENP∽△PFC可知,$\frac{CF}{PF}=\frac{PN}{EN}$,即:$\frac{1}{3-x}=\frac{x}{y}$,
∴$y=-{x}^{2}+3x=-(x-\frac{3}{2})^{2}+\frac{9}{4}$,
当x=$\frac{3}{2}$时,y有最大值,为$\frac{9}{4}$;
∴E的运动的路径长为:$4+2×\frac{9}{4}=\frac{17}{2}$.
点评 本题考查了二次函数的顶点式,相似三角形的判定与性质,极端原理,配方法求二次函数最值等重要知识点,有一定综合性,第三问稍有一点难度.纵观本题,构造相似,利用线段成比例建立方程是求解关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 7$\sqrt{2}$km | B. | 14$\sqrt{2}$km | C. | 7km | D. | 14km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
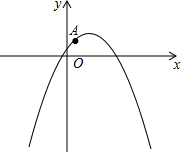 在直角坐标系xoy中,已知抛物线$y=-\frac{{3\sqrt{3}}}{20}({x^2}-\frac{17}{3}x-2)$.
在直角坐标系xoy中,已知抛物线$y=-\frac{{3\sqrt{3}}}{20}({x^2}-\frac{17}{3}x-2)$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
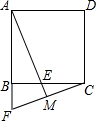 如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )| A. | BE=CE | B. | FM=MC | C. | AM⊥FC | D. | BF⊥CF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x=3y | B. | $\frac{y}{x}$=$\frac{2}{3}$ | C. | $\frac{x}{2}$=$\frac{y}{3}$ | D. | $\frac{x+y}{y}$=$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com