练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在平面直角坐标系中，已知A、B是抛物线上两个不同的点，其中A在第二象限，B在第一象限，

    （1）如图15-1所示，当直线AB与轴平行，AOB=90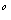，且AB=2时，

         求此抛物线的解析式和A、B两点的横坐标的乘积.

    （2）如图15-2所示，在（1）所求得的抛物线上，当直线AB与轴不平行，AOB仍为90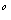时，

         A、B两点的横坐标的乘积是否为常数？如果是，请给予证明，如果不是，请说明理由.

    （3）在（2）的条件下，若直线分别交直线AB，y轴于点P、C，直线AB交y轴于点D，

         且BPC=OCP，求点P的坐标.

           

     


    （1）解析式，

         (2),为常数，（其中另有舍去）

    （3）P

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列几何图形中，既是轴对称图形，又是中心对称图形的是

    A、等腰三角形　　B、正三角形　　　C、平行四边形　　D、正方形

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知直线与双曲线交于A(),B(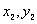)两点（A与B不重合），

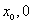       直线AB与轴交于P(),与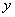轴交于点C.

       (1) 若A,B两点的坐标分别为（1,3），（3，y2）.求点P的坐标；

      （2）若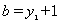,点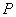的坐标为（6,0），且.求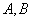两点的坐标；

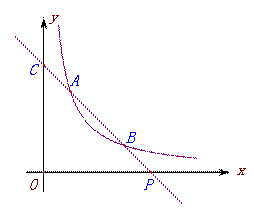
      （3）结合(1),(2)中的结果，猜想并用等式表示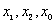之间的关系（不要求证明）.

            

           

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．要使分式有意义，则字母的取值范围是　　　　　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


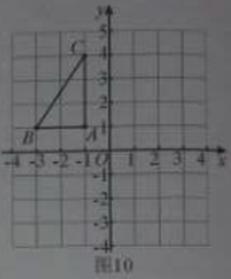
    如图10，在平面直角坐标系中，已知ABC的三个顶点的坐标分别为A(－1，1)，Ｂ（－３,１）Ｃ（－１,４）．

    （１）画出ABC关于ｙ轴对称的；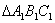

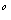    （２）将ABC绕着点Ｂ顺时针旋转90后得到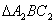，请在图中画出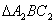，并求出线段ＢＣ旋转过程中所扫过的面积（结果保留）．

     

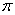    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是(     )

    A.  至少有1个球是黑球          B.至少有1个球是白球               

    C.  至少有2个球是黑球          D.至少有2个球是白球

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若正多边形的一个内角等于140°，则该正多边形的边数是       

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为加强公民的节水意识，合理利用水资源。某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于

    1︰1.5︰2。下图折线表示实行阶梯水价后每月水费y（元）与用水量xm³之间的函数关系。其中线段AB表示第二级阶梯时y与x之间的函数关系

    （1）       写出点B的实际意义;

    （2）       求线段AB所在直线的表达式。

    （3）       某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    比较大小：2_______（填“﹤”，“＝”，“﹥”）.

    查看答案和解析>>

    同步练习册答案