
科目:初中数学 来源: 题型:
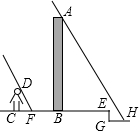 小强在周末搞了一次校外测量活动,他找到了一工厂的烟囱,正好阳光明媚,他就考虑用测量影子的方法去计算这个工厂烟囱的高度AB,但他发现烟囱的影子没有完全落在平地BE上,如图,影子一直落在了前面低洼处的H点,测得当时BE是22米,EG为1.6米,GH为8.4米(点C、F、B、E在和条水平线上,G、H在一条水平线上),他自己的身高CD是1.75米,当时他在阳光下的影长CF为1.6米,求这座烟囱AB的高度为多少米.(如果精确到0.1)
小强在周末搞了一次校外测量活动,他找到了一工厂的烟囱,正好阳光明媚,他就考虑用测量影子的方法去计算这个工厂烟囱的高度AB,但他发现烟囱的影子没有完全落在平地BE上,如图,影子一直落在了前面低洼处的H点,测得当时BE是22米,EG为1.6米,GH为8.4米(点C、F、B、E在和条水平线上,G、H在一条水平线上),他自己的身高CD是1.75米,当时他在阳光下的影长CF为1.6米,求这座烟囱AB的高度为多少米.(如果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两点之间,线段最短 |
| B、过不在同一直线上的三点有且只有一个圆 |
| C、一组对应边相等的两个等边三角形全等 |
| D、对角线相等的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com