练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．

    （1）求证：△ACD∽△BFD；

    （2）若AC=BF，求∠ABD的度数．

    【答案】（1）证明见解析（2）45°

    【解析】试题分析：（1）根据同角的余角相等证得∠DAC=∠FBD，再由∠BDF=∠ADC=90°，根据两角对应相等的两个三角形相似即可得△ACD∽△BFD；（2）由（1）和AC=BF，可判定△ACD≌△BFD，根据全等三角形的性质可得DA=DB，又由AD⊥BC，即可得∠ABD=45°．

    试题解析：

    （1）证明：∵AD⊥BC，BE⊥AC，

    ∴∠DAC+∠C=90°，∠FBD+∠C=90°，

    ∴∠DAC=∠FBD，又∠BDF=∠ADC=90°，

    ∴△ACD∽△BFD；

    （2）解：∵△ACD∽△BFD，AC=BF，

    ∴△ACD≌△BFD，

    ∴DA=DB，又AD⊥BC，

    ∴∠ABD=45°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】肥西素有“淮军故里、改革首县、花木之乡”之美誉，现就肥西以下五个旅游景点进行调查，A．“官亭林海”，B．“三河古镇”，C．“紫蓬山国家森林公园”，D．“小井庄”，E．“刘铭传故居”，为了解学生最喜欢哪一个景点（每人只选取一种），随机抽取了部分学生进行调查，将调查结果绘制成如下不完整的统计表和统计图．根据以上信息解答下列问题：

    （1）本次接受调查的总人数为______人，统计表中m=______，n=______．

    （2）补全条形统计图．

    （3）若把条形统计图改为扇形统计图，则景点“紫蓬山国家森林公园”、“小井庄”、“刘铭传故居”所在扇形的圆心角度数分别是__________、___________、___________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2016广西桂林市）已知任意三角形的三边长，如何求三角形面积？

    古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=（其中a，b，c是三角形的三边长，p=，S为三角形的面积），并给出了证明

    例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：

    ∵a=3，b=4，c=5，∴p==6，∴S===6．

    事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

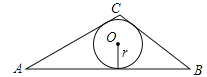
    如图，在△ABC中，BC=5，AC=6，AB=9

    （1）用海伦公式求△ABC的面积；

    （2）求△ABC的内切圆半径r．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地相距60km，甲、乙两人从两地出发相向而行，甲先出发．图中表示两人离A地的距离S（km）与时间t（h）的关系，结合图像回答下列问题：

    （1）表示乙离开A地的距离与时间关系的图像是________(填）；

    甲的速度是__________km/h；乙的速度是________km/h。

    （2）甲出发后多少时间两人恰好相距5km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，抛物线y=﹣x2+2bx﹣3的对称轴为直线x=2．

    （1）求b的值；

    （2）在y轴上有一动点P（0，m），过点P作垂直y轴的直线交抛物线于点A（x1，y1），B（x2，y2），其中x1＜x2．

    ①当x2﹣x1=3时，结合函数图象，求出m的值；

    ②把直线PB下方的函数图象，沿直线PB向上翻折，图象的其余部分保持不变，得到一个新的图象W，新图象W在0≤x≤5时，﹣4≤y≤4，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD的右侧作正方形ADEF，连接CF．

    （1）观察猜想：如图（1），当点D在线段BC上时，

    ①BC与CF的位置关系是：　 　；

    ②BC、CD、CF之间的数量关系为：　 　（将结论直接写在横线上）

    （2）数学思考：如图（2），当点D在线段CB的延长线上时，上述①、②中的结论是否仍然成立？若成立，请给予证明，若不成立，请你写出正确结论再给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】操作探究：已知在纸面上有一数轴(如图所示).

    左右折叠纸面，折痕所在的直线与数轴的交点为“对折中心点”

    操作一：

    (1)左右折叠纸面，使1表示的点与-1表示的点重合，则-3表示的点与 表示的点重合；

    操作二：

    (2)左右折叠纸面，使-1表示的点与3表示的点重合，回答以下问题：

    ①对折中心点所表示的数为 ,对折后5表示的点与数 表示的点重合；

    ②若数轴上A.B两点之间距离为11（A在B的左侧），且A.B两点经折叠后重合，求A.B两点表示的数是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB为⊙O的直径，CD是弦，且ABCD于点E。连接AC、OC、BC。

    （1）求证： ACO=BCD。

    （2）若EB=，CD=，求⊙O的直径。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线，垂足分别为E、F，连接BF、CE.

    (1)求证：四边形BECF是平行四边形；

    (2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

    查看答案和解析>>

    同步练习册答案