
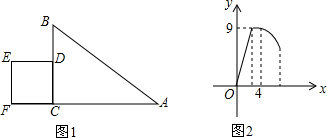
分析 (1)根据图中信息可以知道正方形EFCD的面积,即可求出边长,再根据速度=路程÷时间可以求出速度.
(2)分四种情形:①当0<x≤3时,②当3<x≤4时,③4<x≤7时,④当7<x≤8时,分别求出重合部分面积即可.
(3)利用(2)结论可以得到结论.
解答 解:(1)由图2可知:正方形EFCD的面积为9,所以CD=3,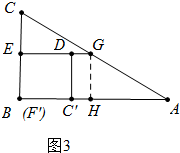
在如图3中,延长ED交AC于G,作GH⊥AB于H,则四边形EGHB是矩形,
∵EG∥AB,
∴$\frac{EG}{AB}$=$\frac{CE}{CB}$,
∴$\frac{EG}{8}$=$\frac{3}{6}$,
∴EG=4,
∴BH=EG=4,
∴V=$\frac{BH}{4}$=1,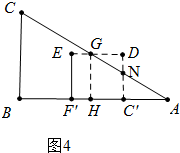
故答案为3,1.
(2)①当0<x≤3时,s=3t.
②当3<x≤4时,s=9.
③4<x≤7时,如图4中,
s=S正方形EFCD-S△DGN=9-$\frac{1}{2}$•[3-$\frac{3}{4}$(8-t)]•$\frac{4}{3}$[3-$\frac{3}{4}$(8-t)]=-$\frac{2}{3}$($\frac{3}{4}$t-3)2+9.
④当7<x≤8时,如图5中,
s=S△AGF′=$\frac{1}{2}$•(11-t)•$\frac{3}{4}$(11-t)=$\frac{3}{8}$(11-t)2.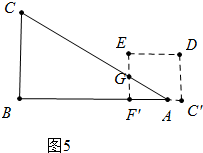 综上所述s=t$\left\{\begin{array}{l}{3t}&{(0<t≤3)}\\{9}&{(3<t≤4)}\\{-\frac{2}{3}(\frac{3}{4}t-3)^{2}+9}&{(4<t≤7)}\\{\frac{3}{8}(11-t)^{2}}&{(7<t≤8)}\end{array}\right.$.
综上所述s=t$\left\{\begin{array}{l}{3t}&{(0<t≤3)}\\{9}&{(3<t≤4)}\\{-\frac{2}{3}(\frac{3}{4}t-3)^{2}+9}&{(4<t≤7)}\\{\frac{3}{8}(11-t)^{2}}&{(7<t≤8)}\end{array}\right.$.
(3)s=6时,3t=6,t=2,
或-$\frac{2}{3}$($\frac{3}{4}$x-3)2+9=6,
t=4+2$\sqrt{2}$或4-2$\sqrt{2}$舍弃.
∴t=2或4+2$\sqrt{2}$时s的值为6.
点评 本题考查动点问题,正方形的性质、勾股定理等知识,解题的关键是读懂题意,学会分类讨论的思想,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com