
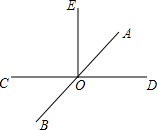
 如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为135°.
如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为135°. 分析 首先根据直线EO⊥CD,可得∠EOD=90°;然后根据AB平分∠EOD,求出∠AOD的大小,进而求出∠BOD的大小即可.
解答 解:∵直线EO⊥CD,
∴∠EOD=90°,
∵AB平分∠EOD,
∴∠AOD=90°÷2=45°,
∴∠BOD=180°-45°=135°.
故答案为:135°.
点评 (1)此题主要考查了垂线的性质和应用,要熟练掌握,解答此题的关键是要明确:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的平分线把这个角分成两个大小相同的角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{106960}{x+500}$-$\frac{50760}{x}$=20 | B. | $\frac{50760}{x}$-$\frac{106960}{x+500}$=20 | ||
| C. | $\frac{106960}{x+20}$-$\frac{50760}{x}$=500 | D. | $\frac{50760}{x}$-$\frac{106960}{x+20}$=500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
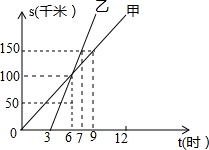 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.回答下列问题:
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{(-8)^{2}}$=-8 | B. | (-$\sqrt{8}$)2=64 | C. | $\sqrt{(-25)^{2}}$=±25 | D. | $\sqrt{9\frac{1}{16}}$=3$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
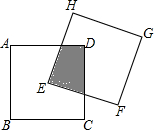 如图,两个边长相等的正方形ABCD和EFGH,将正方形EFGH的顶点E固定在正方形ABCD的对称中心,正方形EFGH绕点E顺时针方向旋转;设旋转的角度为θ(0°≤θ≤360°),两个正方形重叠部分的面积为S,则S与θ的函数关系的大致图象是( )
如图,两个边长相等的正方形ABCD和EFGH,将正方形EFGH的顶点E固定在正方形ABCD的对称中心,正方形EFGH绕点E顺时针方向旋转;设旋转的角度为θ(0°≤θ≤360°),两个正方形重叠部分的面积为S,则S与θ的函数关系的大致图象是( )| A. | 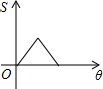 | B. | 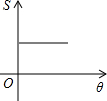 | C. | 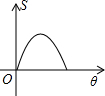 | D. | 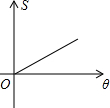 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com