
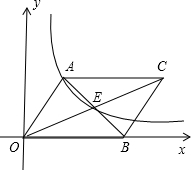
 如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.
如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4. 分析 过A作AD⊥OB于D,过E作EF⊥OB于F,如图,设A(x,$\frac{k}{x}$),B(a,0),根据平行四边形的性质得AE=BE,则可判断EF为△BAD的中位线,于是得到EF=$\frac{1}{2}$AD=$\frac{k}{2x}$,DF=$\frac{1}{2}$(a-x),OF=OD+DF=$\frac{a+x}{2}$,则可表示出E($\frac{a+x}{2}$,$\frac{k}{2x}$),然后根据反比例函数图象上点的坐标特征得到$\frac{a+x}{2}•\frac{k}{2x}=k$,解得a=3x,然后利用平行四边形的面积公式得到关于k的方程,再解方程即可.
解答 解: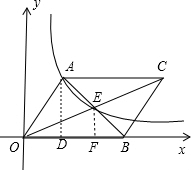 过A作AD⊥OB于D,过E作EF⊥OB于F,如图,
过A作AD⊥OB于D,过E作EF⊥OB于F,如图,
设A(x,$\frac{k}{x}$),B(a,0),
∵四边形AOBC为平行四边形,
∴AE=BE,
∴EF为△BAD的中位线,
∴EF=$\frac{1}{2}$AD=$\frac{k}{2x}$,
∴DF=$\frac{1}{2}$(a-x),
OF=OD+DF=$\frac{a+x}{2}$,
∴E($\frac{a+x}{2}$,$\frac{k}{2x}$),
∵E点在双曲线上,
∴$\frac{a+x}{2}•\frac{k}{2x}=k$,
∴a=3x,
∵平行四边形的面积是12,
∴AD•OB=12,
即$\frac{k}{x}$•a=12,
∴$\frac{k}{x}$•3x=12,
∴k=4.
故答案为4.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了平行四边形的性质.


科目:初中数学 来源: 题型:选择题
| A. | AD=BC | B. | AC=BD | C. | ∠A=∠C | D. | ∠A=∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
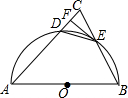 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
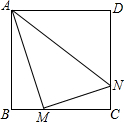 如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.
如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
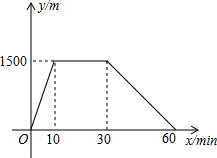 下面的图象反映的过程是:张强跑步去文具店,在文具店买了一些文具,然后散步回家.图中x表示时间,y表示张强离家的距离.
下面的图象反映的过程是:张强跑步去文具店,在文具店买了一些文具,然后散步回家.图中x表示时间,y表示张强离家的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
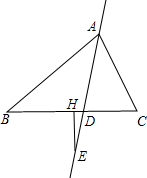 如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.
如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com