
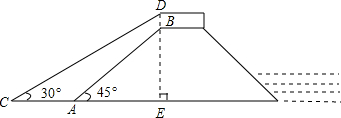
分析 在Rt△BAE中,根据BE=162米,∠BAE=68°,解直角三角形求出AE的长度,然后在Rt△DCE中解直角三角形求出CE的长度,然后根据AC=CE-AE求出AC的长度即可.
解答 解:在Rt△BAE中,∵BE=162米,∠BAE=45°,
∴AE=BE=162米.
在Rt△DCE中,∵DE=176.6米,∠DCE=30°,
∴CE=$\frac{DE}{tan∠DCE}$=$\frac{176.6}{\frac{\sqrt{3}}{3}}$≈305.51(米),
则AC=CE-AE≈305.51-162=143.51≈143.5(米).
答:工程完工后背水坡坡底端水平方向增加的宽度AC约为143.5米.
点评 本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形并解直角三角形.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
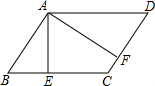 如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.
如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 2π | C. | 6π | D. | 3$\sqrt{5}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com