
 如图,在△ABC中,点O是△ABC的外心,过点O作OD⊥AC,交AC于点D,连接BO,过点A作AE⊥BC,垂足为E,若BO=7,OD=3,则cos∠BAE的值为$\frac{2\sqrt{10}}{7}$.
如图,在△ABC中,点O是△ABC的外心,过点O作OD⊥AC,交AC于点D,连接BO,过点A作AE⊥BC,垂足为E,若BO=7,OD=3,则cos∠BAE的值为$\frac{2\sqrt{10}}{7}$. 分析 连接OA、OC,则OA=OC=OA=7,由OD⊥AC,得出∠AOD=∠COD,由勾股定理求出AD,由圆周角定理得出∠ABC=$\frac{1}{2}$∠AOC=∠AOD,得出cos∠BAE=cos∠AOD,即可求出结果.
解答 解:连接OA、OC,如图所示: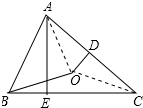
则OA=OC=OA=7,
∵OD⊥AC,
∴∠AOD=∠COD,AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{7}^{2}-{3}^{2}}$=2$\sqrt{10}$,
∵点O是△ABC的外心,
∴∠ABC=$\frac{1}{2}$∠AOC=∠AOD,
∴cos∠BAE=cos∠AOD=$\frac{AD}{OA}$=$\frac{2\sqrt{10}}{7}$;
故答案为:$\frac{2\sqrt{10}}{7}$.
点评 本题考查了三角形的外接圆与外心、圆周角定理、勾股定理、等腰三角形的性质、三角函数;熟练掌握圆周角定理,由圆周角定理得出∠ABC=∠AOD是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买数量(贴) | 单价(元/贴) |
| 不超过10贴(包含10贴) | 9 |
| 超过10贴不超过m贴的部分(15≤m≤30) | 8 |
| 超过m贴的部分 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
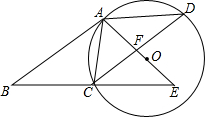 如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.
如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
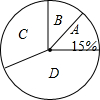 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com