
【题目】在等边![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
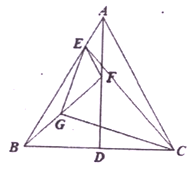
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.
【答案】(1)![]() (2)证明见详解
(2)证明见详解
【解析】
(1)根据等边三角形性质可知BD=![]() BC=
BC=![]() ,利用勾股定理求出AD的长,再利用勾股定理求出BF的值;
,利用勾股定理求出AD的长,再利用勾股定理求出BF的值;
(2)先延长EG至H,使GH=EG,连接BH、CH、FH,构造全等三角形,证四边形BHFE是平行四边形,推出BH∥EF,再由AE=EF,推出AC∥EF,得出AC∥BH,根据平行线的性质推出∠ACB=∠CBH=60°,根据三角形全等的判定和性质得出△CEH是等边三角形,再根据等边三角形性质求得结论即可.
(1)解:∵在等边![]() 中,
中,![]() 于点
于点![]() ,
,![]()
∴AC=BC=AB=![]() ,BD=
,BD=![]() BC=
BC=![]()
∴AD=![]()
∵![]()
∴DF=15-6=9
∴BF=![]()
(2)证明:延长EG至H,使GH=EG,连接BH、CH、FH,
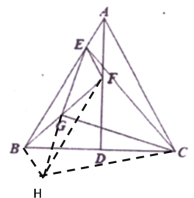
∵点![]() 为
为![]() 的中点,∴BG=FG
的中点,∴BG=FG
∴四边形BHFE是平行四边形,
∴BH=EF,BH∥EF
∵AE=EF ∴BH=AE,∠EAF=∠EFA=∠DAC
∴AC∥EF ∴AC∥BH
∴∠ACB=∠CBH=60°
在△AEC和△BHC中
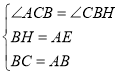
∴△AEC≌△BHC(SAS)
∴∠ACE=∠BCH EC=HC
∴∠ECB+∠ACE=∠ECB+∠BCH=60°即∠ECH=60°
∴△CEH是等边三角形,GH=EG,
∴∠CGE=90°,∠ECG=30°
∴tan30°=EG∶CG=1∶![]()
∴CG=![]() EG
EG


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
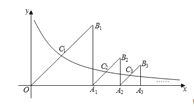
【题目】如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数y![]() (x>0)的图象上.则y1+y2+…+y20的值为____.
(x>0)的图象上.则y1+y2+…+y20的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=2.

(1)求抛物线的解析式;
(2)E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;
(3)设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了适合不同人群的需求,某公司对每日坚果混合装进行改革.甲种每袋装有10克核桃仁,10克巴旦木仁,10克黑加仑;乙种每袋装有20克核桃仁,5克巴旦木仁,5克黑加仑.甲乙两种袋装干果每袋成本价分别为袋中核桃仁、巴旦木仁、黑加仑的成本价之和.已知核桃仁每克成本价0.04元,甲每袋坚果的售价为5.2元,利润率为![]() ,乙种坚果每袋利润率为
,乙种坚果每袋利润率为![]() ,若这两种袋装的销售利润率达到
,若这两种袋装的销售利润率达到![]() ,则该公司销售甲、乙两种袋装坚果的数最之比是____.
,则该公司销售甲、乙两种袋装坚果的数最之比是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
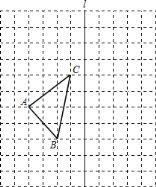
【题目】 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C2;
(3)在(2)的条件下求出线段AC在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
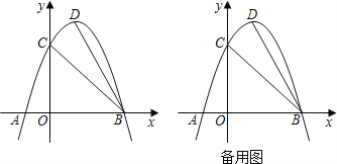
【题目】 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,交y轴正半轴于C点,D为抛物线的顶点,A(-1,0),B(3,0).
(1)求出二次函数的表达式.
(2)点P在x轴上,且∠PCB=∠CBD,求点P的坐标.
(3)在x轴上方抛物线上是否存在一点Q,使得以Q,C,B,O为顶点的四边形被对角线分成面积相等的两部分?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
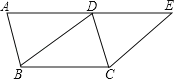
【题目】如图,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD.
(1)求证:四边形BCED是平行四边形;
(2)若DA=DB=2,cosA=![]() ,求点B到点E的距离.
,求点B到点E的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
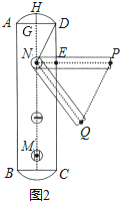
【题目】小明家的门框上装有一把防盗门锁(如图1),其平面结构图如图2所示,锁身可以看成由两条等弧![]() ,
,![]() 和矩形
和矩形![]() 组成的,
组成的,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .已知
.已知![]() 的弓形高
的弓形高![]() ,
,![]() ,
,![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 顺时针旋转至
顺时针旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在的圆相切,且
所在的圆相切,且![]() ,
,![]() .
.
(1)求![]() 所在圆的半径;
所在圆的半径;
(2)求线段![]() 的长度.(
的长度.(![]() ,结果精确到
,结果精确到![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com