
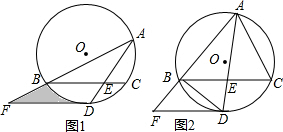
分析 (1)连结OD,如图1,由角平分线定义得∠BAD=∠CAD,则根据圆周角定理得到$\widehat{BD}$=$\widehat{CD}$,再根据垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是根据切线的判定定理即可判断DF为⊙O的切线;
(2)连结OB,OD交BC于P,作BH⊥DF于H,如图1,先证明△OBD为等边三角形得到∠ODB=60°,OB=BD=2$\sqrt{3}$,易得∠BDF=∠DBP=30°,根据含30度的直角三角形三边的关系,在Rt△DBP中得到PD=$\frac{1}{2}$BD=$\sqrt{3}$,PB=$\sqrt{3}$PD=3,接着在Rt△DEP中利用勾股定理计算出PE=2,由于OP⊥BC,则BP=CP=3,所以CE=1,然后利用△BDE∽△ACE,通过相似比可得到AE=$\frac{5\sqrt{7}}{7}$,再证明△ABE∽△AFD,利用相似比可得DF=12,最后根据扇形面积公式,利用S阴影部分=S△BDF-S弓形BD=S△BDF-(S扇形BOD-S△BOD)进行计算;
(3)连结CD,如图2,由$\frac{AB}{AC}$=$\frac{4}{3}$可设AB=4x,AC=3x,设BF=y,由$\widehat{BD}$=$\widehat{CD}$得到CD=BD=2$\sqrt{3}$,先证明△BFD∽△CDA,利用相似比得到xy=4,再证明△FDB∽△FAD,利用相似比得到16-4y=xy,则16-4y=4,然后解方程易得BF=3.
解答 证明:(1)连结OD,如图1,
∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴$\widehat{BD}$=$\widehat{CD}$,
∴OD⊥BC,
∵BC∥EF,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,如图1,
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=30°,
∴∠BOD=2∠BAD=60°,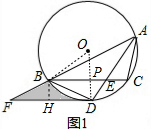
∴△OBD为等边三角形,
∴∠ODB=60°,OB=BD=2$\sqrt{3}$,
∴∠BDF=30°,
∵BC∥DF,
∴∠DBP=30°,
在Rt△DBP中,PD=$\frac{1}{2}$BD=$\sqrt{3}$,PB=$\sqrt{3}$PD=3,
在Rt△DEP中,∵PD=$\sqrt{3}$,DE=$\sqrt{7}$,
∴PE=$\sqrt{(\sqrt{7})^{2}-(\sqrt{3})^{2}}$=2,
∵OP⊥BC,
∴BP=CP=3,
∴CE=3-2=1,
易证得△BDE∽△ACE,
∴AE:BE=CE:DE,即AE:5=1:$\sqrt{7}$,
∴AE=$\frac{5\sqrt{7}}{7}$
∵BE∥DF,
∴△ABE∽△AFD,
∴$\frac{BE}{DF}$=$\frac{AE}{AD}$,即$\frac{5}{DF}$=$\frac{\frac{5\sqrt{7}}{7}}{\frac{12\sqrt{5}}{7}}$,解得DF=12,
在Rt△BDH中,BH=$\frac{1}{2}$BD=$\sqrt{3}$,
∴S阴影部分=S△BDF-S弓形BD
=S△BDF-(S扇形BOD-S△BOD)
=$\frac{1}{2}$•12•$\sqrt{3}$-$\frac{60•π•(2\sqrt{3})^{2}}{360}$+$\frac{\sqrt{3}}{4}$•(2$\sqrt{3}$)2
=9$\sqrt{3}$-2π;
(3)连结CD,如图2,由$\frac{AB}{AC}$=$\frac{4}{3}$可设AB=4x,AC=3x,设BF=y,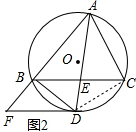 ∵$\widehat{BD}$=$\widehat{CD}$,
∵$\widehat{BD}$=$\widehat{CD}$,
∴CD=BD=2$\sqrt{3}$,
∵∠F=∠ABC=∠ADC,
∵∠FDB=∠DBC=∠DAC,
∴△BFD∽△CDA,
∴$\frac{BD}{AC}$=$\frac{BF}{CD}$,即$\frac{2\sqrt{3}}{3x}$=$\frac{y}{2\sqrt{3}}$,
∴xy=4,
∵∠FDB=∠DBC=∠DAC=∠FAD,
而∠DFB=∠AFD,
∴△FDB∽△FAD,
∴$\frac{DF}{AF}$=$\frac{BF}{DF}$,即$\frac{8-y}{y+4x}$=$\frac{y}{8-y}$,
整理得16-4y=xy,
∴16-4y=4,解得y=3,
即BF的长为3.
点评 本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和切线的判定定理;会计算不规则几何图形的面积;会灵活运用相似三角形的判定与性质计算线段的长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、D、E在⊙O上,点B、C在AD上,BC=2,△BCE为等边三角形,且∠AOD=120°.
如图,点A、D、E在⊙O上,点B、C在AD上,BC=2,△BCE为等边三角形,且∠AOD=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
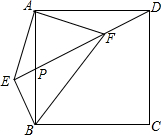 如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE,FA⊥AE交DP于点F,连接BF、FC.若AE=4,则FC=4$\sqrt{2}$.
如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE,FA⊥AE交DP于点F,连接BF、FC.若AE=4,则FC=4$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com