

分析 (1)图①中,连接CD,先证明△CDM≌△BDN得CM=BN,即可证明BM-CM=MN=$\sqrt{2}$DM.
(2)图②中,结论:BM+CM=$\sqrt{2}$DM,先证明△CDM≌△BDN得CM=BN由BM+CM=BM+BN=MN=$\sqrt{2}$DM得出结论.图③中,结论:CM-BM=$\sqrt{2}$DM,先证明△CDM≌△DN得CM=BN由CM-BM=BN-BM=MN=$\sqrt{2}$DM得出结论.
(3)在图①②③中利用已经证明的结论分别求出DM即可.
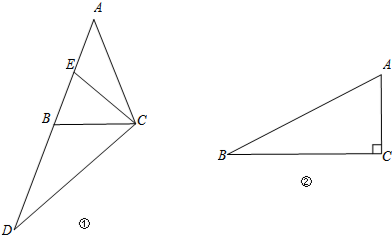
解答 (1)证明:如图①中,连接CD
∵CA=CB,∠ACB=90°,AD=DB,
∴CD=AD=DB,∠A=∠BC=45°,CD⊥AB,
∵∠MDN=90°,∠DNM=∠ABC=45°,
∴∠DMN=∠DNM=45°,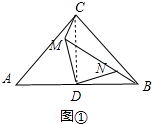
∴DM=DN,MN=$\sqrt{2}$DM,
∵∠CDB=∠MDN=90°,
∴∠CDM=∠BDN,
在△DCM和△DBN中,
$\left\{\begin{array}{l}{DC=DB}\\{∠CDM=∠BDN}\\{DM=DN}\end{array}\right.$,
∴△CDM≌△BDN,
∴CM=BN,
∴BM-CM=BM-BN=MN=$\sqrt{2}$DM.
(2)在图②中,结论:BM+CM=$\sqrt{2}$DM.理由如下:
证明:连接CD,∵CA=CB,∠ACB=90°,AD=DB,
∴CD=AD=DB,∠A=∠ABC=45°,CD⊥AB,
∵∠MDN=90°,∠DNM=∠ABC=45°,
∴∠DMN=∠DNM=45°,
∴DM=DN,MN=$\sqrt{2}$DM,
∵∠CDB=∠MDN=90°
∴∠CDM=∠BDN,
在△DCM和△DBN中
$\left\{\begin{array}{l}{DC=DB}\\{∠CDM=∠BDN}\\{DM=DN}\end{array}\right.$,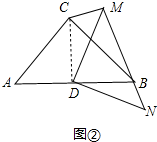
∴△CDM≌△BDN,
∴CM=BN,
∴BM+CM=BM+BN=MN=$\sqrt{2}$DM
在图③中,结论:CM-BM=$\sqrt{2}$DM,理由如下:
证明:连接CD,∵CA=CB,∠ACB=90°,AD=DB,
∴CD=AD=DB,∠A=∠ABC=45°,CD⊥AB,
∵∠MDN=90°,∠DNM=∠ABC=45°,
∴∠DMN=∠DNM=45°,
∴DM=DN,MN=$\sqrt{2}$DM,
∵∠CDB=∠MDN=90°,
∴∠CDM=∠BDN,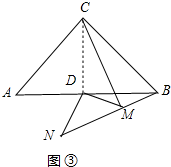
在△DCM和△DBN中
$\left\{\begin{array}{l}{DC=DB}\\{∠CDM=∠BDN}\\{DM=DN}\end{array}\right.$,
∴△CDM≌△DN,
∴CM=BN,
∴CM-BM=BN-BM=MN=$\sqrt{2}$DM.
(3)在图①中∵∠DCB+∠DBC=90°
∴∠DCB+∠CBM+∠DBN=90°,
由(1)可知:△CDM≌△BDN,
∴∠DCM=∠DBN,
∴∠DCB+∠CBM+∠DCM=90°,
∴∠MCB+∠CBM=90°,
∴∠CMB=90°,
∵tan∠BCM=$\frac{3}{4}$,可以假设CM=3k,BM=4k,
∵S△ACB=$\frac{25}{2}$,∴BC=CA=5,
∵CM2+BM2=BC2
∴(3k)2+(4k)2=25,
k=1,
∴MC=3,BM=4,
∵BM-CM=$\sqrt{2}$DM,
∴DM=$\frac{\sqrt{2}}{2}$,
在图②中,∵∠CMD=∠N=45°,∠DMN=45°,
∴∠CMB=90°,
∵tan∠BCM=$\frac{3}{4}$,可以假设BM=3k,CM=4k,
∵CM2+BM2=BC2
∴(3k)2+(4k)2=25,
k=1,
∴MC=4,BM=3,
∵BM+CM=$\sqrt{2}$DM,
∴DM=$\frac{7\sqrt{2}}{2}$,
在图③中,∵∠CMD=∠N=45°,∠DMN=45°,
∴∠CMN=∠CMB=90°,
∵tan∠BCM=$\frac{3}{4}$,可以假设BM=3k,CM=4k,
∵CM2+BM2=BC
∴(3k)2+(4k)2=25,
k=1,
∴MC=4,BM=3,
∵CM-BM=$\sqrt{2}$DM,
∴DM=$\frac{\sqrt{2}}{2}$,
综上所述:DM=$\frac{\sqrt{2}}{2}$或$\frac{7\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$或$\frac{7\sqrt{2}}{2}$.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质,解题的关键是三个图形中△CDM和△BDN都是全等的,证明方法类似,形变结论不变,在求DM时考虑问题必须全面.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
 用一个平面按如图所示的方式“切割”正方体,可以得到一个正方形的截面,将该正方体的侧面展开,“切割线”(虚线)位置正确的是( )
用一个平面按如图所示的方式“切割”正方体,可以得到一个正方形的截面,将该正方体的侧面展开,“切割线”(虚线)位置正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
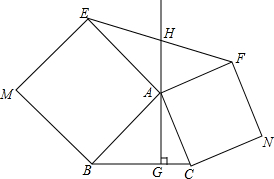 同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.
同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F,若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为4.
如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F,若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com