练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．用一个平面按如图所示的方式“切割”正方体，可以得到一个正方形的截面，将该正方体的侧面展开，“切割线”（虚线）位置正确的是（　　）
    A．B．C．D．

    分析 将ABCD作为面向自己的面，展开即可．

    解答 解：将ABCD作为面向自己的面展开，
    即可得到，
    故选C．

    点评 本题考查了几何体的展开图，熟悉正方体的展开图，并逐步培养自己的空间意识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．列式表示下列问题中y与x的函数关系式，并指出哪些是正比例函数．
    （1）圆的半径为x，周长为y．
    （2）每本练习本0.5元，购买练习本的总费用y（元）与购买练习本的本数x（本）．
    （3）汽车以80千米/时的速度匀速行驶，行驶时间为x小时，所行驶的路程为y千米．
    （4）某人一个月的收人为3500元，这个人的总收入y（元）随工作时间x（月）的变而币变化．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．若抛物线y=ax2经过点（-3，6）．
    （1）求此二次函数的表达式：
    （2）说出这个二次函数图象的顶点坐标、对称轴、开口方向和图象的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，AB和CD相交于O，∠A=∠B，试说明必有∠C=∠D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．2014年底，某市机动车保有量已达120万辆，至2015年年底，该市机动车保有量达到138万辆．
    （1）按这样的增长速度，2016年底将达到158.7万辆；
    （2）如果该市在2017年底机动车保有量控制在166.98万辆，那么，2016年、2017年这两年的平均增长率最多是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

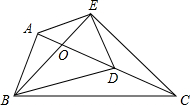    9．如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的三角板如图放置，使三角板斜边的两个端点分别与A、D重合，E为直角顶点，连接EC、BE．
    （1）求证：BE=CE；
    （2）延长CE、BA交于F，设BE与AC相交于点O，则OE与EF的关系应为OE=OF；
    （3）在（2）的条件下，已知AF=2，AO=1，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．直角△ABC中，BC=AC，D为AB的中点，点N为平面内一点，连接DN，BN，过点D作DN的垂线交BN于点M，且∠DNM=∠ABC，连接CM．
    （1）如图①，求证：BM-CM=$\sqrt{2}$DM．
    （2）在图②，图③两种情况下，线段BM．CM．DM又有怎样的数量关系？请写出你的猜想，不需要证明；
    （3）若S△ABC=$\frac{25}{2}$，tan∠BCM=$\frac{3}{4}$，则DM=$\frac{\sqrt{2}}{2}$或$\frac{7\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知点P1（a-1，4）和P2（2，b）关于x轴对称，则（a+b）2015的值为（　　）
    A．72014B．1C．-1D．（-3）2014

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．“十字相乘法”能把二次三项式分解因式，对于形如ax2+bxy+cy2的x，y二次三项式来说，方法的关键是把x2项系数a分解成两个因数a1，a2的积，即a=a1•a2，把y2项系数c分解成两个因数，c1，c2的积，即c=c1•c2，并使a1•c2+a2•c1正好等于xy项的系数b，那么可以直接写成结果：ax2+bxy+cy2=（a1x+c1y）（a2x+c2y）
    例：分解因式：x2-2xy-8y2
    解：如右图，其中1=1×1，-8=（-4）×2，而-2=1×（-4）+1×2∴x2-2xy-8y2=（x-4y）（x+2y）
    而对于形如ax2+bxy+cy2+dx+ey+f的x，y的二元二次式也可以用十字相乘法来分解，
    如图1，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np=b，pk+qj=e，mk+nj=d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式=（mx+py+j）（nx+qy+k）；

    例：分解因式：x2+2xy-3y2+3x+y+2
    解：如图2，其中1=1×1，-3=（-1）×3，2=1×2；
    而2=1×3+1×（-1），1=（-1）×2+3×1，3=1×2+1×1；∴x2+2xy-3y2+3x+y+2=（x-y+1）（x+3y+2）
    请同学们通过阅读上述材料，完成下列问题：
    （1）分解因式：6x2-7xy+2y2=（2x-y）（3x-2y）x2-6xy+8y2-5x+14y+6=（x-2y-2）（x-4y-3）
    （2）若关于x，y的二元二次式x2+7xy-18y2-5x+my-24可以分解成两个一次因式的积，求m的值．
    （3）已知x，y为整数，且满足x2+3xy+2y2+2x+4y=-1，求x，y．

    查看答案和解析>>

    同步练习册答案