
【题目】如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比函数y=-![]() 和y=
和y=![]() (m>0)的图象上.
(m>0)的图象上.

(1)当AB=BC时,求m的值。
(2)连结OA,OD.当OD平方∠AOC时,求△AOD的周长.

【答案】(1)4 (2)10+2![]()
【解析】
(1)把A点坐标代入反比例函数式![]() ,求出a值,则A的横坐标可知,由条件知AB=BC,求出OC的长度,则求出D点的坐标,把D点坐标代入
,求出a值,则A的横坐标可知,由条件知AB=BC,求出OC的长度,则求出D点的坐标,把D点坐标代入![]() ,则可求出m的值.
,则可求出m的值.
(2)现知A点坐标,则可求出OA的长度,根据角平分线的定义和两直线平行内错角相等,等量代换得出 ∠ADO=∠AOD ,所以AO=AD=5,则OC的长度可求,现知DC的长度,用勾股定理即可求出OD的长度,则△AOD的周长可求.
(1)当y=4时,a=![]() =-3,
=-3,
∴OB=3.
∵矩形ABCD,且AB=BC,
∴AB=BC=CD=4,
∴OC=1,
∴D(1,4),
∴m=4.
(2)∵ ∠ABO=90°,A(-3,4),
∴OA=5.
∵OD平分∠AOC,
∴∠AOD=∠DOC.
∵AD∥BC,
∴∠ADO=∠DOC,
∴∠ADO=∠AOD,
∴DA=OA=5,
∴OC=2.
∵∠OCD=90°,
∴OD![]() ,
,
∴△AOD的周长是10+2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的。
是“中心轴对称”的。
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,![]() 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的![]() 倍,行驶相同的路程
倍,行驶相同的路程![]() 千米,G377少用
千米,G377少用![]() 个小时。
个小时。
(1)求D31的平均速度。
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为![]() 元/张,G377票件为
元/张,G377票件为![]() 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的国球是乒乓球,世界上乒乓球板的拍形大体上可以归为三类:圆形、方形和异形,绝大多数的横板与中国式的直板都是圆型的.如图,李明同学自制一块乒乓球拍,正面是半径为8 cm的⊙O,弧AB的长为4πcm,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为( )

A. (32+48π)cm2 B. (16π﹣32)cm2 C. 64πcm2 D. (48π﹣32)cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.
(1)求证:四边形FCBG是矩形.
(2)己知AB=10,![]() .
.
①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S2.若EG=2FH,求S1+S2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板的三个内角分别是90![]() ,45
,45![]() ,45
,45![]() 和90
和90![]() ,60
,60![]() ,30
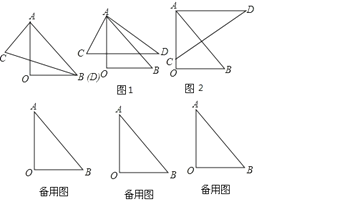
,30![]() ,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0
,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0![]() <α<180
<α<180![]() )
)
(1)如图1中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图2中,当α=___时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数。(写出三个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1上图形有6个小圆,第2个图形有10个小圆,和3个图形有16个小圆,第4个图形有24个小圆,…依此规律,第7个图形的小圆的个数是_____,第n个图形的小圆的个数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
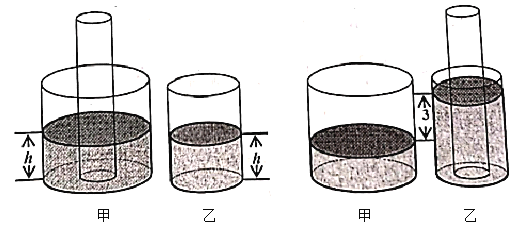
【题目】如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体, 甲、乙容器的内底面半径分别为![]() 和
和![]() ,现将一个半径为
,现将一个半径为![]() 的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为
的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为![]() (如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高
(如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高![]() (如图乙).
(如图乙).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含![]() 的代数式表示).
的代数式表示).
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com