Question

【题目】如图1，AB为⊙O的直径，C为⊙O上一点，CD切⊙O于点C， ，BD交⊙O于点E，连CE

（1）求证：

（2）若，求的值

Answer 1

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）连接AC，OC，由AB是⊙O的直径，得到∠A+∠ABC=90°，由垂直的定义得到∠DCB+∠CBD=90°，根据切线的性质得到∠CDB=∠A，即可得到结论；

（2）连接AE，由勾股定理得到BC=2，由AB为⊙O的直径，得到∠ACB=90°=∠AEB，推出△BCD∽△CED，根据相似三角形的性质得到ED= =8，BE=6AB=＝10，由三角函数的定义即可得到结论．

试题解析：（1）证明：连接AC，OC，

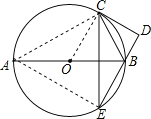
∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠A+∠ABC=90°，

∵BD⊥CD，

∴∠D=90°，

∴∠DCB+∠CBD=90°，

∵CD切⊙O于点C，

∴∠CDB=∠A，

∴∠ABC=∠DBC；

（2）解：连接AC，AE，

∵∠D=90°，

∴BC=2，

∵AB为⊙O的直径，

∴∠ACB=90°=∠AEB，

∴∠BAC+∠ABC=90°=∠DBC+∠BCD，

∴∠BCD=∠BAC=∠CED，

∴△BCD∽△CED，

∴，

∴ED==8，BE=6，

∵△BCD∽△BAC，

∴，

∴AB=＝10，

∴AE==8，

∴cos∠ECB=cos∠BAE=．