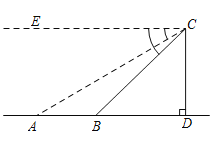
【题目】如图，直升飞机在大桥
上方
点处测得
，
两点的俯角分别为31°和45°．若飞机此时飞行高度
为
，且点，，
在同一条直线上，求大桥的长．（精确到
）（参考数据：
，
，
）
科目：初中数学 来源： 题型：
【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，
其中正确的是（ ）
A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
与反比例函数
的图象交于A（m，6），B（3，n）两点.
（1）求一次函数的解析式；
（2）求
的面积；
（3）根据图象直接写出
的x的取值范围
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某科技公司接到一份新型高科技产品紧急订单，要求在
天内（含天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了该种产品
件，以后每天生产的产品都比前一天多
件．由于机器损耗等原因，当日生产的产品数量达到
件后，每多生产一件，当天生产的所有产品平均每件成本就增加元．
（1）设第
天生产产品
件，求出与之间的函数解析式，并写出自变量的取值范围．
（2）若该产品每件生产成本（日生产量不超过件时）为
元，订购价格为每件
元，设第天的利润为
元，试求与之间的函数解析式，并求该公司哪一天获得的利润最大，最大利润的是多少？
（3）该公司当天的利润不低于
元的是哪几天？请直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某部门为新的生产线研发了一款机器人，为了解它的操作技能情况，在相同条件下与人工操作进行了抽样对比.过程如下，请补充完整.收集数据对同一个生产动作，机器人和人工各操作10次，测试成绩(十分制)如下：
整理、描述数据按如下分段整理、描述这两组样本数据：
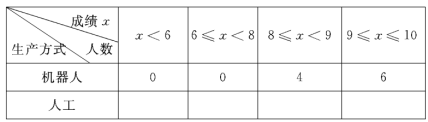
(说明：成绩在9.0分及以上为操作技能优秀，8≤r<9分为操作技能良好，6≤r<8分为操作技能合格，6.0分以下为操作技能不合格)
分析数据两组样本数据的平均数、中位数、众数和方差如下表所示：
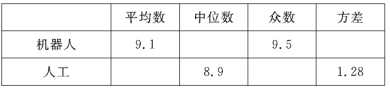
得出结论：
(1)请结合数据分析写出机器人在操作技能方面两条优点：
(2)如果生产出一个产品，需要完成同样的操作200次，估计机器人生产这个产品达到操作技能优秀的次数为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
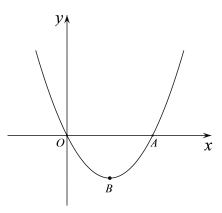
【题目】如图，抛物线y=x2+mx（m<0）交x轴于O，A两点，顶点为点B．
（1）求△AOB的面积（用含m的代数式表示）；
（2）直线y=kx+b（k＞0）过点B，且与抛物线交于另一点D（点D与点A不重合），交y轴于点C．过点C作CE∥AB交x轴于点E．
（ⅰ） 若∠OBA=90°，2<
<3，求k的取值范围；
（ⅱ） 求证：DE∥y轴．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知甲、乙两辆汽车分别从
、
两地同时匀速出发，甲车开往地，乙车开往地，设甲、乙两车距地的路程分别为
、
（单位：
），甲车的行驶时间为
（单位：
）．若甲车的速度为
，与之间的对应关系如下表：
| 2 | 5 |
| 560 | 320 |
（1）分别求出、与之间的函数关系式；（不写的取值范围）
（2）当为何值时，甲、乙两辆汽车相遇？
（3）当两车距离小于
时，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的图象与
轴交于点
(点
在点
的左侧)，与
轴交于点
，顶点为
．
(Ⅰ)当
时，求二次函数的最大值；
(Ⅱ)当
时，点
是轴上的点，
，将点
绕点
顺时针旋转90°得到点
，点恰好落在该二次函数的图象上，求
的值；
(Ⅲ)
是该二次函数图象上的一点，在(Ⅱ)的条件下，连接
，
，使
，求点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
