
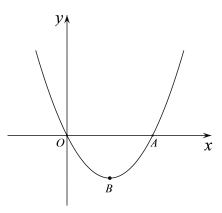
【题目】如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.
(1)求△AOB的面积(用含m的代数式表示);
(2)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范围;
<3,求k的取值范围;
(ⅱ) 求证:DE∥y轴.
【答案】(1)-![]() ;(2)(ⅰ)1<k<2;(ⅱ)见解析
;(2)(ⅰ)1<k<2;(ⅱ)见解析
【解析】
(1)已知y![]() x2
x2![]() mx,将其化为顶点式,可求得B点坐标,令x2
mx,将其化为顶点式,可求得B点坐标,令x2![]() mx=0可求得OA长,即可用m表示出△OAB的面积.
mx=0可求得OA长,即可用m表示出△OAB的面积.
(2)(ⅰ)如图所示,过点B作BF⊥x轴于点F,可证得△EOC∽△AFB,得出![]() ,已知
,已知![]() ,则
,则![]() ,(1)中已得出点B的坐标,且∠OBA
,(1)中已得出点B的坐标,且∠OBA![]() 90°,得△OAB为等腰直角三角形,列出关于m的方程,求得m值,进而求出BF长,得到OC的取值范围,即为直线y
90°,得△OAB为等腰直角三角形,列出关于m的方程,求得m值,进而求出BF长,得到OC的取值范围,即为直线y![]() kx
kx![]() b与y轴截距的取值范围,由已知求得的点B坐标,代入直线y
b与y轴截距的取值范围,由已知求得的点B坐标,代入直线y![]() kx
kx![]() b,即可得出k的取值范围.
b,即可得出k的取值范围.
(ⅱ)将用m表示的B点坐标代入直线y![]() kx
kx![]() b中,可将b用m,k表示出来,C点坐标可用m,k表示出来,令抛物线解析式与直线BC解析式相等得到交点D的坐标,再求得AB解析式,根据CE∥AB,即可求得直线CE解析式,得到E点坐标,若点D,E的横坐标相同,即可证得DE∥y轴.
b中,可将b用m,k表示出来,C点坐标可用m,k表示出来,令抛物线解析式与直线BC解析式相等得到交点D的坐标,再求得AB解析式,根据CE∥AB,即可求得直线CE解析式,得到E点坐标,若点D,E的横坐标相同,即可证得DE∥y轴.
(1)y![]() x2
x2![]() mx=
mx=![]()
∴点B的坐标为B![]()
由x2![]() mx=0,
mx=0,
得x=0,或x=-m,
∴A(-m,0)
∴OA=-m
∴S△OAB=![]()
(2)(ⅰ)如图所示,过点B作BF⊥x轴于点F
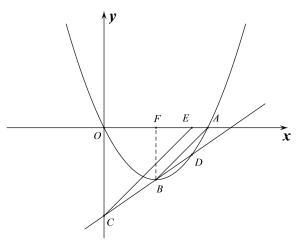
则∠AFB=∠EOC=90°
∵CE∥AB
∴∠OEC=∠FAB
∴△EOC∽△AFB
∴![]()
∵![]()
∴![]()
∵抛物线的顶点坐标为B(![]() ,
,![]() ),∠OBA
),∠OBA![]() 90°
90°
∴△OAB为等腰直角三角形
∴![]()
∵m≠0
∴m=-2
∴B(1,-1)
∴BF=1
∴2<OC<3
∵点C为直线y![]() kx
kx![]() b与y轴交点
b与y轴交点
∴2<-b<3
∵直线y![]() kx
kx![]() b(k>0)过点B
b(k>0)过点B
∴k![]() b=-1
b=-1
∴-b=k+1
∴2<k+1<3
∴1<k<2
故答案为:1<k<2
(ⅱ)∵直线y![]() kx
kx![]() b(k>0)过点B(
b(k>0)过点B(![]() ,
,![]() )
)
∴![]()
∴![]()
∴y![]() kx
kx![]()
![]()
∴C(0,![]() )
)
由x2![]() mx
mx![]() kx
kx![]()
![]() ,得
,得
x2![]() (m-k)x-
(m-k)x-![]() =0
=0
△=(m-k)2+4![]() =k2
=k2
解得x1![]()
![]() ,x2
,x2![]()
![]() ,
,
∵点D不与点B重合
∴点D的横坐标为![]()
设直线AB的表达式为y=px+q,则:
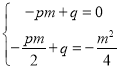
解得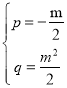
∴直线AB的表达式为y=![]() +
+![]()
∵直线CE∥AB,且过点C,
∴直线CE的表达式为y=![]() +
+![]()
当y=0时,x=![]()
∴E(![]() ,0)
,0)
∴点D,E的横坐标相同
∴DE∥y轴


科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.我市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如图不完整的统计图.
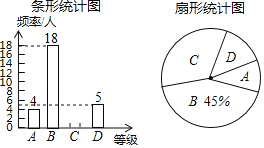
根据所给信息,解答以下问题:
(1)本次抽样调查抽取了 名学生的成绩;在扇形统计图中,D对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为___________米(精确到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
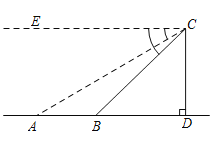
【题目】如图,直升飞机在大桥![]() 上方
上方![]() 点处测得
点处测得![]() ,
,![]() 两点的俯角分别为31°和45°.若飞机此时飞行高度
两点的俯角分别为31°和45°.若飞机此时飞行高度![]() 为
为![]() ,且点
,且点![]() ,
,![]() ,
,![]() 在同一条直线上,求大桥
在同一条直线上,求大桥![]() 的长.(精确到
的长.(精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了强化学生的环保意识,某校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,两个队学生的复赛成绩(满分10分)如图所示:
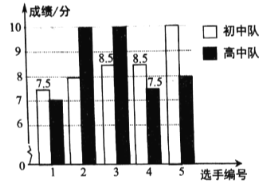
(1)根据图示填写下表:
平均分 | 中位数 | 众数 | 方差 | |
初中队 | 8.5 | 0.7 | ||
高中队 | 8.5 | 10 |
(2)小明同学说:“这次复赛我得了8分,在我们队中排名属中游偏下!”小明是初中队还是高中队的学生?为什么?
(3)结合两队成绩的平均分、中位数和方差,分析哪个对的复赛成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园安全问题受到全社会的广泛关注,省教育局要求各学校加强对学生的安全教育,某中学为了了解学生对校园安全知识的了解程度(程度分为:A.十分熟悉、B.了解较多、C.了解较少、D.不了解),随机抽取了该校部分学生进行调查,统计整理并绘制成如下两幅不完整的统计图.

根据以上信息解答下列问题:
(1)本次接受调查的学生共有________人,扇形统计图中A部分所对应的扇形圆心角是______;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,估计该校学生中对校园安全知识的了解程度达到A和B的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BC,垂足为E,若BD=![]() ,BC=6,则AB=( )
,BC=6,则AB=( )

A.![]() B.2C.
B.2C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 在半圆上,连结
在半圆上,连结![]() ,
,![]() ,且
,且![]() .连结
.连结![]() ,
,![]() 是
是![]() 边上的高,过点
边上的高,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值.
的值.
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
①若![]() ,在点
,在点![]() 运动过程中,当四边形
运动过程中,当四边形![]() 的其中一边长是
的其中一边长是![]() 的2倍时,求所有满足条件的
的2倍时,求所有满足条件的![]() 长.
长.
②连结![]() ,当
,当![]() 的面积是
的面积是![]() 的面积的3倍时,求
的面积的3倍时,求![]() 的值(请直接写出答案).
的值(请直接写出答案).
图1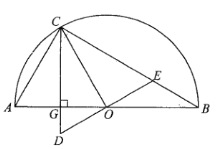 图2
图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com