
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BC,垂足为E,若BD=![]() ,BC=6,则AB=( )
,BC=6,则AB=( )

A.![]() B.2C.
B.2C.![]() D.3
D.3
【答案】B
【解析】
过点D作DH⊥AB,交BA的延长线于H,可证四边形BEDH是正方形,可得BD=![]() BE,DE=HD,∠HDE=∠ADC=90°,由“ASA”可证△ADH≌△CDE,可得AH=CE=2,即可求解.
BE,DE=HD,∠HDE=∠ADC=90°,由“ASA”可证△ADH≌△CDE,可得AH=CE=2,即可求解.
解:如图,过点D作DH⊥AB,交BA的延长线于H,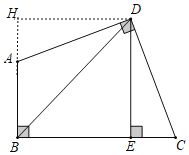
∵∠ABC=∠ADC=90°,DH⊥AB,DE⊥BC,
∴四边形BEDH是矩形,
∵BD平分∠ABC,
∴∠DBE=45°,
∴∠DBE=∠BDE=45°,
∴BE=DE,
∴四边形BEDH是正方形,
∴BD=![]() BE,DE=HD,∠HDE=∠ADC=90°,
BE,DE=HD,∠HDE=∠ADC=90°,
∴HD=DE=HB=BE=4,∠HDA=∠CDE,
又∵∠H=∠DEC=90°,
∴△ADH≌△CDE(ASA),
∴CE=AH=BC-BE=6-4=2,
∴AB=BH-AH=4-2=2,
故选:B.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】小明准备给长![]() 米,宽
米,宽![]() 米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形
米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形![]() 和
和![]() 均为正方形,且各有两边与长方形边重合;矩形
均为正方形,且各有两边与长方形边重合;矩形![]() (区域II)是这两个正方形的重叠部分,如图所示.
(区域II)是这两个正方形的重叠部分,如图所示.
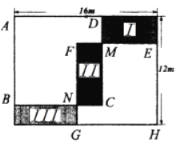
(1)若花卉均价为![]() 元
元![]() ,种植花卉的面积为
,种植花卉的面积为![]()
![]() ,草坪均价为
,草坪均价为![]() 元
元![]() ,且花卉和草坪栽种总价不超过
,且花卉和草坪栽种总价不超过![]() 元,求
元,求![]() 的最大值.
的最大值.
(2)若矩形![]() 满足
满足![]() .
.
①求![]() ,
,![]() 的长.
的长.
②若甲、乙、丙三种花卉单价分别为![]() 元
元![]() ,
,![]() 元
元![]() ,
,![]() 元
元![]() ,且边
,且边![]() 的长不小于边
的长不小于边![]() 长的
长的![]() 倍.求图中I、II、III三个区域栽种花卉总价
倍.求图中I、II、III三个区域栽种花卉总价![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
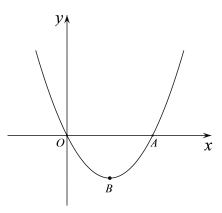
【题目】如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.
(1)求△AOB的面积(用含m的代数式表示);
(2)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范围;
<3,求k的取值范围;
(ⅱ) 求证:DE∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
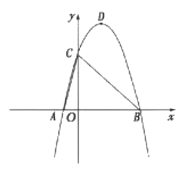
【题目】如图,在平面直角坐标系中,抛物线![]() 经过A(-1,0)B(4,0),C(0,4)三点.
经过A(-1,0)B(4,0),C(0,4)三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)将(1)中的抛物线向下平移![]() 个长度单位,再向左平移h(h>0)个长度单位,得到新抛物线.若新抛物线的顶点
个长度单位,再向左平移h(h>0)个长度单位,得到新抛物线.若新抛物线的顶点![]() 在△ABC内,求h的取值范围;
在△ABC内,求h的取值范围;
(3)点P为线段BC上的一动点(点P不与点B,C重合),过点P作x轴的垂线交(1)中的抛物线于点Q,当△PQC与△ABC相似时,求△PQC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
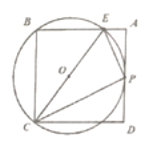
【题目】如图,已知在正方形![]() 中,
中,![]() ,
,![]() 是线段
是线段![]() 上的一动点,连接
上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .以
.以![]() 为直径作
为直径作![]() ,当点
,当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,对应点
时,对应点![]() 也随之运动,则点
也随之运动,则点![]() 运动的路程长度为____________.
运动的路程长度为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 及一次函数
及一次函数![]() ,将该二次函数在
,将该二次函数在![]() 轴上方的图象沿
轴上方的图象沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线
轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线![]() 与新函数图象有4个交点时,
与新函数图象有4个交点时,![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com