练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．在等腰△ABC中，∠A=4∠B，则∠C的度数为（　　）
    A．30°B．60°C．30°或80°D．60°或80°

    分析 根据三角形的内角和定理得∠A+∠B+∠C=180°，而∠A=4∠B=∠C，则有∠B+4∠B+4∠B=180°，或∠A=4∠B=4∠C，则有∠B+4∠B+∠B=180°，解方程即可得到∠C的度数．

    解答 解：∵∠A+∠B+∠C=180°，∠A=4∠B，
    ∴当∠A=∠C时，
    即4∠B+4∠B+∠B=180°，
    ∴∠B=20°，
    ∴∠C=80°，
    当∠B=∠C时，
    即∠B+4∠B+∠B=180°，
    ∴∠B=30°，
    ∴∠C=30°，
    综上所述：∠C的度数为30°或80°．
    故选C．

    点评 本题考查了等腰三角形的性质，三角形的内角和定理，熟练掌握等腰三角形的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如图，一块矩形的土地，长48m，宽24m，要在它的中央划一块矩形的草地，四周铺上花砖路，路面宽都相等，草地占去矩形土地的$\frac{5}{9}$，则花砖路面的宽为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．在锐角的内部引射线，当n=1，n=2时，图中小于180°角的个数及规律如表，请你在表中空白处填出射线为3和n的情形．
     图形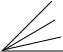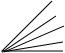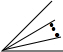    
     n 1 2 3 n
     个数及规律 3=1+2=$\frac{2×3}{2}$ 6=1+2+3=$\frac{3×4}{2}$10=1+2+3+4=$\frac{4×5}{2}$ 1+2+3+…+n+1=$\frac{（n+1）（n+2）}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在正方形ABCD中，DE为正方形的外角∠ADF的角平分线，点G在线段AD上，过点G作PG⊥DE于点P，连接CP，过点D作DQ⊥PC于点Q，交射线PG于点H．

    （1）如图1，若点G与点A重合．
    ①依题意补全图1；
    ②判断DH与PC的数量关系并加以证明；
    （2）如图2，若点H恰好在线段AB上，正方形ABCD的边长为1，请写出求DP长的思路（可以不写出计算结果）．

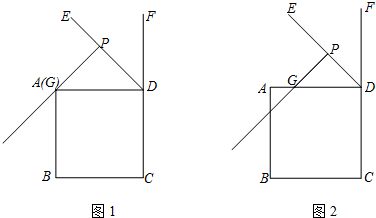
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，点A、B、C、D、E、F为⊙O的六等分点，动点P从圆心O出发，沿OE弧EFFO的路线做匀速运动，设运动的时间为t，∠BPD的度数为y，则下列图象中表示y与t之间函数关系最恰当的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，BD是△ABC的角平分线，DE⊥AB于点E．△ABC的面积为20，AB=12，BC=8，则DE的长为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解下列方程
    （1）x2+8=4$\sqrt{2}$x
    （2）2（x-3）2=-x（3-x）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．在数轴上画出表示下列各数的点，并用“＜”号把它们连接起来．-2，-1$\frac{1}{2}$，2，0，2$\frac{1}{2}$，-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．用计算机处理数据，为了防止数据输入出错，某研究室安排两位程序操作员各输入一遍，比较两人的输入是否一致．两人各输入3120个数据，已知甲的输入速度是乙的2倍，结果甲比乙少用2小时输完，这两位程序操作员每小时各能输入多少个数据？

    查看答案和解析>>

    同步练习册答案