
1+
| ||
| 2 |
| 13 |
| 2 |
| 3 |
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 13 |
| ||
| 2 |
| ||
| 2 |
| 13 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 3 |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
| A、824×104 |
| B、8.24×105 |
| C、8.24×106 |
| D、0.824×107 |
查看答案和解析>>
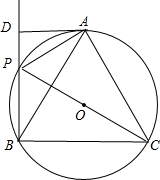
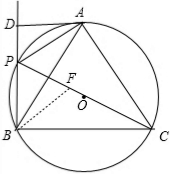
科目:初中数学 来源: 题型:
查看答案和解析>>
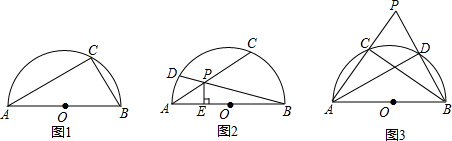
科目:初中数学 来源: 题型:

| PQ |
| AB |

查看答案和解析>>
科目:初中数学 来源: 题型:
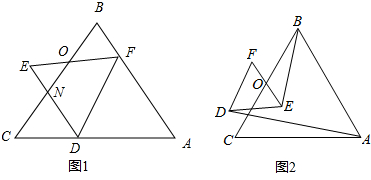
查看答案和解析>>
科目:初中数学 来源: 题型:
 《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?
《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com