Question

7．如图，AB是半圆0的直径，过C是半圆上的一点，过点C作CD⊥AB于D，AC=2$\sqrt{10}$cm，AD：DB=4：1，求CD的长．

Answer 1

分析 连接BC，设AD=4x，根据题意用x表示出DB、AB，根据射影定理求出x，得到AD的长，根据勾股定理计算即可．

解答 解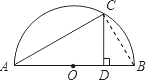：连接BC，
设AD=4x，则DB=x，
∴AB=5x，
∵AB是半圆0的直径，
∴∠ACB=90°，又CD⊥AB，
∴AC²=AD•AB，即（2$\sqrt{10}$）²=4x•5x，
解得，x=$\sqrt{2}$，
∴AD=4$\sqrt{2}$，
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=2$\sqrt{2}$．

点评 本题考查的是射影定理和勾股定理的应用，掌握直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项、每一条直角边是这条直角边在斜边上的射影和斜边的比例中项是解题的关键．