
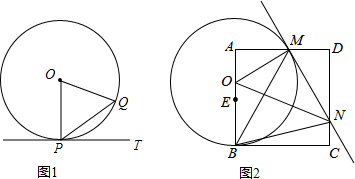
分析 探究1:如图1,作直径PH,连结HQ,根据圆周角定理得到∠PQH=90°,则∠HPQ+∠H=90°,再根据切线的性质得∠HPT+∠QPT=90°,则∠H=∠QPT,由三角形外角性质得∠POQ=∠H+∠OQO=2∠H,于是有∠TPQ=$\frac{1}{2}$∠POQ;
探究2:如图2,作BP⊥MN于N,利用探究1的结论得到∠CBM=$\frac{1}{2}$BOM,∠PMB=$\frac{1}{2}$∠BOM,则∠CBM=∠PMB,再利用AD∥BC得到∠CBM=∠AMB,所以∠AMB=∠PMB,接着利用“AAS”证明△BMA≌△BMP得到AM=PM,BA=BP,由于AB=BC,则BP=BC,然后根据“HL”证明Rt△BNP≌Rt△BNC得到PN=PC,则MN=PM+PN=AM+CN.
解答 解:探究1:如图1,∠TPQ=$\frac{1}{2}$∠POQ.理由如下: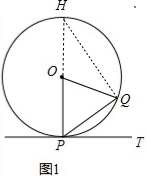
作直径PH,连结HQ,
∵PH为直径,
∴∠PQH=90°,
∴∠HPQ+∠H=90°,
∵直线PT和⊙O相切于点P,
∴HP⊥PT,
∴∠HPT+∠QPT=90°,
∴∠H=∠QPT,
∵OP=OQ,
∴∠H=∠OQH,
∴∠POQ=∠H+∠OQO=2∠H,
∴∠TPQ=$\frac{1}{2}$∠POQ;
(2)探究2:MN=AM+CN.理由如下:
如图2,作BP⊥MN于N,
∵四边形ABCD为正方形,
∴∠OBC=90°,
∴BC为⊙O的切线,
∴∠CBM=$\frac{1}{2}$BOM,
∵MN为⊙O的切线,
∴∠PMB=$\frac{1}{2}$∠BOM,
∴∠CBM=∠PMB,
∵AD∥BC,
∴∠CBM=∠AMB,
∴∠AMB=∠PMB,
在△BMA和△BMP中,
$\left\{\begin{array}{l}{∠BAM=∠BPM}\\{∠BMA=∠BMP}\\{BM=BM}\end{array}\right.$,
∴△BMA≌△BMP(AAS),
∴AM=PM,BA=BP,
∵AB=BC,
∴BP=BC,
在Rt△BNP和Rt△BNC中,
$\left\{\begin{array}{l}{BP=BC}\\{BN=BN}\end{array}\right.$,
∴Rt△BNP≌Rt△BNC(HL),
∴PN=PC,
∴MN=PM+PN=AM+CN.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、切线的判定与性质和正方形的性质;会利用三角形全等解决线段相等的问题;利用探究1的结论是解决探究2的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
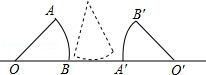 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com