
����Ŀ��ij�ض����������أ�ѧ����Ⱦ�϶࣬��ɲ���ѧУ�ż٣�Ϊ��Ԥ�����У��ؽ����Ҫ���У���з��أ�ijѧУ�ƻ�������ĩ�����Ҽ�����������������ҩ�����������мס�����λ��ʦ�����нӸù��������ס�������ʦ����6Сʱ�������ȫ��������������ʦ������4Сʱ��ʣ�µ�����ʦ����������9Сʱ��ɣ���ס�������ʦ������ɸù����������Сʱ��
 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��1����һ�κ���y=kx+b�Ĺ�ϵʽ��
��2�����ͼ��ֱ��д������kx+b��![]()
![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
��3������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=6��AB��BC��AD��CD����BAD=60������M��N�ֱ���AB��AD���ϣ���AM��MB=AN��ND=1��2����tan��MCN=

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
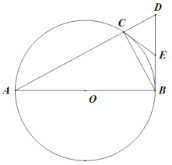
����Ŀ����ͼ����֪![]() �ڽ���
�ڽ���![]() ��
��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
��1��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ����֤��
����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ����
����![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������������ƽ���ߵĽ��㣬�����������ĵ�һ��ֱ���������ཻ��������֮����߶ΰ���������ηֳ�����ͼ�Σ�����һ��ͼ����ԭ���������ƣ���������߶ν�����������εġ������ߡ���
��1���ȱ������Ρ������ߡ�������Ϊ�� ����
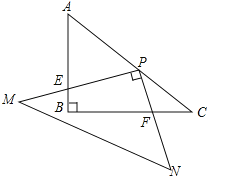
��2����ͼ����ABC�У�AB=AC����D��AC�ϣ���BD=BC=AD����֤��BD����ABC�ġ������ߡ���
��3����Rt��ABC�У���C=90�㣬AC=4��BC=3��E��F�ֱ��ڱ�AC��BC�ϣ���EF����ABC�ġ������ߡ�����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
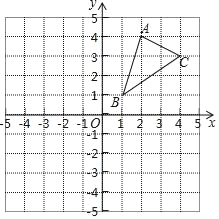
����Ŀ����1���뻭����ABC����x��ԳƵġ�A1B1C1����д����A1�����꣮
��2���뻭����ABC�Ƶ�B��ʱ����ת90���ġ�A2BC2��
��3�������2����C����ת��C2����������·����������������źͦУ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�������ѵ��������ͬ�����¸����5�Σ��ɼ�ͳ�����±���
����� | 7 | 8 | 9 | 10 |
��������Ӧ�����Ĵ��� | 2 | 2 | 0 | 1 |
��������Ӧ�����Ĵ��� | 1 | 3 | 1 | 0 |
(1)��ס�����������ɼ���ƽ������
(2)�ס��������У�˭������ɼ����ȶ�Щ?��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ʱ��
ʱ��![]() ________��
________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵXOY�У���A��0��a����B��b��0���ң�a��4��2+![]() =0����ABΪֱ�DZ�������Rt��ABC����CAB=90�㣬AB=AC��
=0����ABΪֱ�DZ�������Rt��ABC����CAB=90�㣬AB=AC��
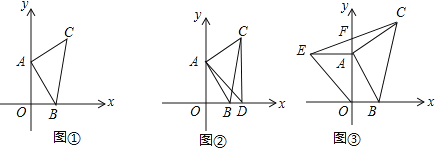
��1����C�����ꣻ
��2����ͼ����C����CD��X����D������AD������ADC�Ķ�����
��3����ͼ���ڣ�1���У���A��Y�����˶�����OAΪֱ�DZ�������Rt��OAE������EC����Y����F������A�����˶�������S��AOB��S��AEF��ֵ�Ƿ�ᷢ���仯�����û�б仯����ֱ��д�����ǵı�ֵ�� ��������Ҫ�����̻�˵�����ɣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com