
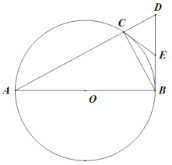
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)![]() 为
为![]() 的中点,连结
的中点,连结![]() ,求证:
,求证:![]() 是
是![]() 的切线.
的切线.
(2)若![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)证明见解析(2)30°
【解析】
(1)想要证明CE是⊙O的切线,证明∠OCE=90°即可,连接半径OC,根据同圆的半径相等和直角三角形斜边中线等于斜边一半可得:∠EBC+∠OBC=∠ECB+∠OCB,则∠OCE=∠OBE=90°,可得结论;
(2)设CD=m,则AC=3m,证明△ACB∽△BCD,列比例式可得:BC=![]() m,利用三角函数定义可得结论.
m,利用三角函数定义可得结论.
(1)连接OC,
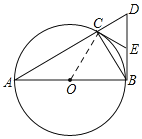
∵![]() 为
为![]() 的直径,
的直径,
∴∠ACB=∠DCB=90°,
∵![]() 为
为![]() 的中点,
的中点,
∴BE=CE,
∴∠EBC=∠ECB,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠ECB+∠OCB=∠EBC+∠OBC,
∵![]() ,
,
∴∠OCE=∠OBE=90°,
∴![]() 是
是![]() 的切线.
的切线.
(2)设CD=m,则AC=3m,
∵△ACB≌△BCD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =30°.
=30°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
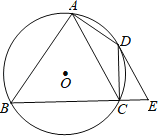
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
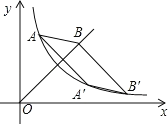
【题目】如图,已知反比例函数y=![]() (x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A'(4,b)与点B'均在反比例函数的图象上,点B在直线y=x上,四边形AA'B'B是平行四边形,则B点的坐标为______.
(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A'(4,b)与点B'均在反比例函数的图象上,点B在直线y=x上,四边形AA'B'B是平行四边形,则B点的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(![]() ,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
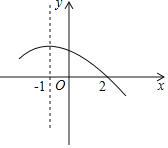
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县冬季流感严重,学生感染较多,造成不少学校放假,为了预防流感,县教体局要求各校进行防控.某学校计划利用周末将教室及公共环境进行“喷药消毒”,现有甲、乙两位老师主动承接该工作,若甲、乙两老师合作6小时可以完成全部工作;若甲老师单独做4小时后,剩下的乙老师单独做还需9小时完成.求甲、乙两老师单独完成该工作各需多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
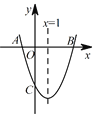
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com