
分析 (1)根据给定的等式依次写出第5、6个等式,由此即可得出结论;
(2)分析等式各分母与an下标之间的关系,由此即可得出第n个等式;
(3)根据变化规律an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)将代数式进行分解,再运用分式的加、减法即可求出结论.
解答 解:(1)∵a1=$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),a2=$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),a3=$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$),a4=$\frac{1}{7×9}$=$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$),
∴a5=$\frac{1}{9×11}$=$\frac{1}{2}$($\frac{1}{9}$-$\frac{1}{11}$),a6=$\frac{1}{11×13}$=$\frac{1}{2}$($\frac{1}{11}$-$\frac{1}{13}$).
故答案为:$\frac{1}{11×13}$;$\frac{1}{2}$($\frac{1}{11}$-$\frac{1}{13}$).
(2)观察发现等式的分母为(2n-1)(2n+1)、2n-1以及2n+1,
∴an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$).
故答案为:$\frac{1}{(2n-1)(2n+1)}$;$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$).
(3)原式=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)+…+$\frac{1}{2}$($\frac{1}{4029}$-$\frac{1}{4031}$)+$\frac{1}{2}$($\frac{1}{4031}$-$\frac{1}{4033}$),
=$\frac{1}{2}$×1-$\frac{1}{2}$×$\frac{1}{4033}$,
=$\frac{2016}{4033}$.
点评 本题考查了规律型中数字的变化类以及分式的加减法,解题的关键是:(1)观察给定等式依次写出第5、6个等式;(2)观察等式找出变化规律an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);(3)根据变化规律an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)将代数式进行分解.


科目:初中数学 来源: 题型:解答题
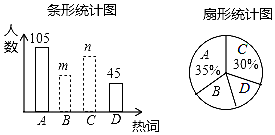 2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:
2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
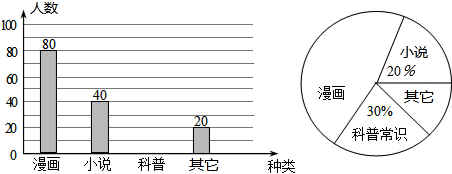
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°
如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
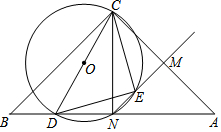 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.
已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
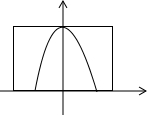 如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )
如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )| A. | 2.52米 | B. | 2.88米 | C. | 2.97米 | D. | 3.12米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com