
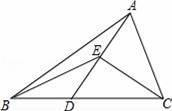
如图,D为△ABC的BC边上的任意一点,E为AD的中点,△BEC的面积为5,则△ABC的面积为 .

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
已知:多项式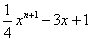 的次数的3.
的次数的3.
(1)填空: = ;
= ;
(2)直接判断:单项式 与单项式
与单项式 是否为同类项 (填“是”或“否”);
是否为同类项 (填“是”或“否”);
|
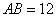 cm,点
cm,点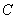 是直线
是直线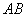 上一点,且
上一点,且 ·
·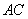 ,若点
,若点 是
是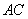 的中点,求线段
的中点,求线段 的长.
的长. 第26题图
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
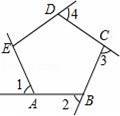

A.80° B.100° C.108° D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1225,
…
(1)根据上述格式反应出的规律填空:952= 5 ,
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果 ,
(3)这种简便计算也可以推广应用:
①个位数字是5的三位数的平方,请写出1952的简便计算过程及结果,
②十位数字相同,且个位数字之和是10的两个两位数想成的算式,请写出89×81的简便计算过程和结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com