
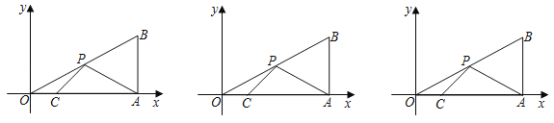
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB��90����AC��BC��6��D���߶�BC�ϣ�E���߶�AD��һ�㣮����CEΪֱ�DZߣ�CΪֱ�Ƕ��㣬��CE���·�������ֱ����ECF������BF��
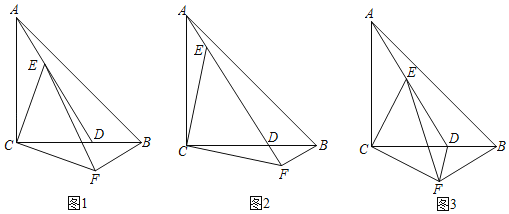
��1����ͼ1����֤��AE��BF��
��2����A��E��F���㹲��ʱ����ͼ2����BF��2����AF�ij���
��3����ͼ3������BAD��15��������DF����E�˶���ʹ�á�ACE��30��ʱ������DEF�������
���𰸡���1������������2��AF��2![]() ����3��S��EDF��3
����3��S��EDF��3![]() ��3��
��3��
��������
��1����ͼ1�У�֤����ACE�ա�BCF��SAS�����ɽ�����⣻
��2������ȫ�������ε����ʣ�֤����ACD=��DFB=90���������ù��ɶ������ɽ�����⣻
��3����ͼ3�У���FH��BC��H��֤����BCF�ǵ�Ϊ30���ĵ��������Σ����CF��FB��FH������S��EDF=S��ECD+S��CDF-S��ECF���㼴�ɣ�
��1��֤������ͼ1�У�
�ߡ�ACB����ECF���ǵ��������Σ�
��CA��CB��CE��CF����ACB����ECF��90����
���ACE����BCF��
���ACE�ա�BCF��SAS����
��AE��BF��
��2����ͼ2�У�
��CA��CB��6����ACB��90����
��AB��6![]() ��
��
�ߡ�ACE�ա�BCF��
���CAD����DBF��
�ߡ�ADC����BDF��
���ACD����DFB��90����
��AF��![]() ��
��![]() ��2
��2![]() ��
��
��3����ͼ3�У���FH��BC��H��
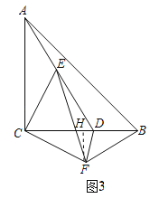
�ߡ�ACE����CAE��30����
��AE��EC��
�ߡ�ACE�ա�BCF��
��BF��AE��CF��CE��
��CF��BF����FCB����CBF��30����
��FC��FB��FH��BC��
��CH��BH��3��FH��![]() ��CF��BF��2
��CF��BF��2![]() ��
��
�ߡ�CED����CAE+��ACE��60������ECD��90����30����60����
���ECD�ǵȱ������Σ�
��EC��CF��CD��2![]() ��
��
��S��EDF��S��ECD+S��CDF��S��ECF��![]() ����2
����2![]() ��2+
��2+![]() ��2
��2![]() ��
��![]() ��
��![]() ��2
��2![]() ��2
��2![]() ��3
��3![]() ��3��
��3��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BD�ཻ�ڵ�O����D=��C�����������ĸ��������Բ���ʹ��ADO�ա�BCO���ǣ�������

A. AD=BC B. AC=BD C. OD=OC D. ��ABD=��BAC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ʵ�������ϵ�����ú���֪ʶ�����������⣺
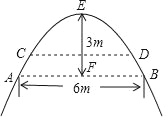
��ͼ����ij�����ϵ�һ���������ι��ţ����Ŷ�����E������ˮ��ľ���EFΪ3��ʱ��ˮ���ABΪ6�ף�һ���������ˮ���ǣ�ˮ����ȱ�ΪCD����CD=2![]() �ף���ʱˮλ�����˶����ף�
�ף���ʱˮλ�����˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ����������һ������ƽ�����ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn�����4�������εı߳���__��Sn��ֵΪ__��
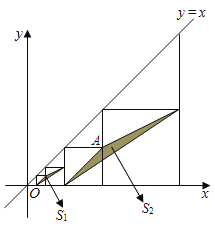
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��OAB��ֱ�Ƕ���A��x����������ϣ�������B��������Ϊ2![]() ����B��60����OC��
����B��60����OC��![]() AC��
AC��
��1����д��A��B��C��������ꣻ
��2����P��б��OB�ϵ�һ�����㣬����PAC���ܳ�����СֵΪ���٣�
��3������P��OB���е㣬��E��AO���ϣ�����OPE��PE���ۣ�ʹ�õ�O����O'������O'E��ACʱ��������ƽ�����Ƿ����һ��Q��ʹ����BAQ�ա�O��PE�������ڣ���ֱ��д��Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC�͡�ACB��ƽ�����ཻ�ڵ�O������O��EF��BC��AB��E����AC��F������O��OD��AC��D�������ĸ����ۣ�
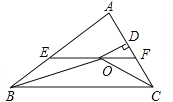
��EF=BE+CF��
�ڡ�BOC=90��+![]() ��A��
��A��
�۵�O����ABC���ߵľ�����ȣ�
����OD=m��AE+AF=n����![]() ��
��
������ȷ�Ľ�����____��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CA=CB��CD=CE����ACB=��DCE=����
��1����֤��BE=AD��

��2������=90��ʱ��ȡAD��BE���е�ֱ�Ϊ��P��Q������CP��CQ��PQ����ͼ�ڣ��ж���CPQ����״��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ��(����![]() )������һ��������ijһֱ���ϵ���ʻ�����У�����������صľ���
)������һ��������ijһֱ���ϵ���ʻ�����У�����������صľ���![]() (ǧ��)����ʻʱ��
(ǧ��)����ʻʱ��![]() (ʱ)֮��ĺ�����ϵ������ͼ���ṩ����Ϣ����������˵��������������ʻ��140ǧ�ף�����������ʻ;��ͣ����1Сʱ����������������ʻ�����е�ƽ���ٶ�Ϊ30ǧ��/ʱ��������������6Сʱ��9Сʱ֮����ʻ���ٶ�����С.������ȷ��˵������( )
(ʱ)֮��ĺ�����ϵ������ͼ���ṩ����Ϣ����������˵��������������ʻ��140ǧ�ף�����������ʻ;��ͣ����1Сʱ����������������ʻ�����е�ƽ���ٶ�Ϊ30ǧ��/ʱ��������������6Сʱ��9Сʱ֮����ʻ���ٶ�����С.������ȷ��˵������( )

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪��E����AOB��ƽ������һ�㣬EC��OA��ED��OB������ֱ�ΪC��D����֤��

��1����ECD=��EDC��
��2��OE��CD�Ĵ�ֱƽ���ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com