
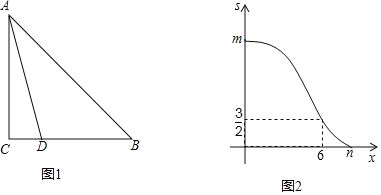
【题目】如图1,已知Rt△ABC中,∠C=90°,点D在BC上,且CD=2,连接AD将Rt△ACD沿射线CB方向平移,得到Rt△A'C'D',C'到达B点时,停止平移,设平移距离为x,△A'C'D'与△ABC重合面积为S,且x与S的函数关系式如图2所示,(0<x≤6,与6<x≤n所对应的解析式不同).
(1)m= ,n= .
(2)写出S与x的函数关系式,直接写出x对应的取值范围.
【答案】(1)6,8;(2)S=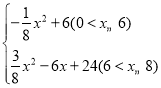 .
.
【解析】
(1)当点D到达点B的位置时,x=6,即BD=6,则BC=8,此时BD重合,S=![]() ,解得:C′M=
,解得:C′M=![]() ,MC′∥AC,
,MC′∥AC,![]() ,即
,即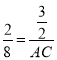 ,解得:AC=6,m=S△ABD=
,解得:AC=6,m=S△ABD=![]() ×2×6=6,即可求解;
×2×6=6,即可求解;
(2)①S=S四边形MND′C′=S△MBC′-S△NBD′=![]() C′MC′B-
C′MC′B-![]() NHBD′,②如图2,S=
NHBD′,②如图2,S=![]() BC′MC′;即可求解.
BC′MC′;即可求解.
(1)当点D到达点B的位置时,x=6,即BD=6,则BC=8,
此时BD重合,S=![]() =
=![]() BC′×MC′=
BC′×MC′=![]() 2×MC′,解得:C′M=
2×MC′,解得:C′M=![]() ,
,
∵MC′∥AC,∴![]() ,即
,即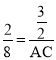 ,解得:AC=6,
,解得:AC=6,
m=S△ABD=![]() 2×6=6,
2×6=6,
C'到达B点时,停止平移,故n=BC=8,
(2)①如图1,当0<x≤6时,CC′=x,BD′=8﹣2﹣x=6﹣x,作MH⊥BC于点H,
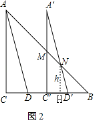
设NH=h,S=S四边形MND′C′=S△MBC′﹣S△NBD′=![]() C′MC′B﹣
C′MC′B﹣![]() NHBD′,
NHBD′,
tan∠ADC=![]() =
=![]() =tan∠ND′H,则HD′=
=tan∠ND′H,则HD′=![]() h,同理BH=
h,同理BH=![]() h,则BD′=
h,则BD′=![]() h﹣
h﹣![]() h=h=6﹣x=NH,
h=h=6﹣x=NH,
同理CM=BC′tan∠B=![]() (8﹣x),
(8﹣x),
故S=![]() (8﹣x)2﹣
(8﹣x)2﹣![]() ×(6﹣x)2=﹣
×(6﹣x)2=﹣![]() x2+6;
x2+6;
②如图2,当6<x≤8时,
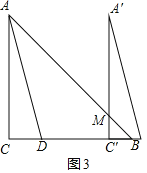
S=![]() BC′MC′=
BC′MC′=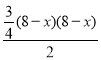 =
=![]() x2﹣6x+24;
x2﹣6x+24;
故S=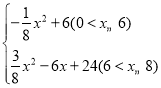 .
.


科目:初中数学 来源: 题型:
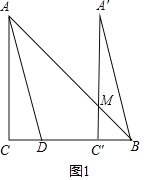
【题目】如图,已知等边三角形ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
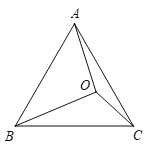
(1)依题意补全图形;
(2)若OA=![]() ,OB=
,OB=![]() ,OC=1,求∠OCM的度数.
,OC=1,求∠OCM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
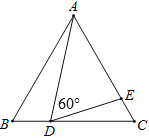
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为()
A. (4,-3) B. (-4,3) C. (-3,4) D. (-3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ,
,![]() ,
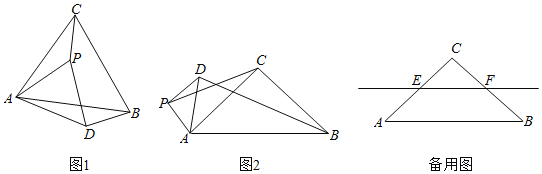
,![]() .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当![]() 时,
时,![]() 的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当![]() 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时
时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
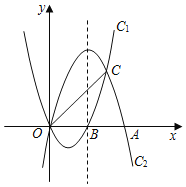
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,AC与BD交于点O, N是AO的中点,点M在BC边上,且BM=3, P为对角线BD上一点,当对角线BD平分∠NPM时,PM-PN值为( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com