
分析 多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解答 证明:因为一块地板由三种正多边形的小木板镶嵌而成,这三种正多边形的边数分别为a,b,c,
可得:$180°-\frac{360°}{a}+180°-\frac{360°}{b}+180°-\frac{360°}{c}=360°$,
180°=$\frac{360°}{a}+\frac{360°}{b}+\frac{360°}{c}$,
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2}$.
点评 本题考查了镶嵌,关键是根据多边形位于同一顶点处的几个角之和能为360°即可.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
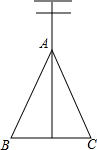 如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.
如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com