
【题目】在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
【答案】3或 ![]()
【解析】解:连结CP,PB的延长线交⊙C于P′,如图,∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2 ,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A= ![]() =
= ![]() ,
,
∴PA的长为3或 ![]() .
.
故答案为3或 ![]() .
.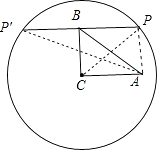
连结CP,PB的延长线交⊙C于P′,如图,先计算出CB2+PB2=CP2 , 则根据勾股定理的逆定理得∠CBP=90°,再根据垂径定理得到PB=P′B=4,接着证明四边形ACBP为矩形,则PA=BC=3,然后在Rt△APP′中利用勾股定理计算出P′A= ![]() ,从而得到满足条件的PA的长为3或
,从而得到满足条件的PA的长为3或 ![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表. 调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |

请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有人,a+b= , m=;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥x轴,与对角线AC、边OC分别交于点E、点F.若B1E:B1F=1:3,点B1的横坐标为m,求点B1的纵坐标,并直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )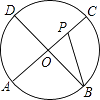
A.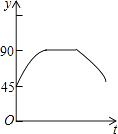
B.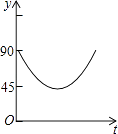
C.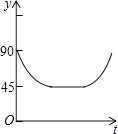
D.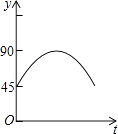
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;
(4)在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( ) 
A.△ADE∽△ABC
B.△ADE∽△ACD
C.△ADE∽△DCB
D.△DEC∽△CDB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为60元的保温饭盒,投放市场进行试销售,按物价部门规定,其销售单价不低于成本,但销售利润不高于65%,市场调研发现,保温饭盒每天的销售数量y(个)与销售单价x(元)满足一次函数关系;当销售单价为70元时,销售数量为160个;当销售单价为80元时,销售数量为140个(利润率= ![]() )
)
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,公司每天获得利润最大,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米. 
(1)在如图的坐标系中,求抛物线的表达式;
(2)若洪水到来是水位以0.2米/时的速度上升,从正常水位开始,再过几小时能到达桥面?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com