
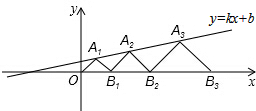
 如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014). 分析 先求出直线y=kx+b的解析式,求出直线与x轴、y轴的交点坐标,求出直线与x轴的夹角的正切值,分别过等腰直角三角形的直角顶点向x轴作垂线,然后根据等腰直角三角形斜边上的高线与中线重合并且等于斜边的一半,利用正切值列式依次求出三角形的斜边上的高线,即可得到A3的坐标,进而得出各点的坐标的规律.
解答 解:∵A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{k+b=1}\\{\frac{7}{2}k+b=\frac{3}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=\frac{4}{4}}\end{array}\right.$,
∴直线解析式为y=$\frac{1}{5}$x+$\frac{4}{5}$;
设直线与x轴、y轴的交点坐标分别为N、M,
当x=0时,y=$\frac{4}{5}$,
当y=0时,$\frac{1}{5}$x+$\frac{4}{5}$=0,解得x=-4,
∴点M、N的坐标分别为M(0,$\frac{4}{5}$),N(-4,0),
∴tan∠MNO=$\frac{MO}{NO}$=$\frac{\frac{4}{5}}{4}$=$\frac{1}{5}$,
作A1C1⊥x轴与点C1,A2C2⊥x轴与点C2,A3C3⊥x轴与点C3, ∵A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),
∵A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),
∴OB2=OB1+B1B2=2×1+2×$\frac{3}{2}$=2+3=5,
tan∠MNO=$\frac{{A}_{3}{C}_{3}}{N{C}_{3}}$=$\frac{{A}_{3}{C}_{3}}{4+5+{B}_{3}{C}_{3}}$=$\frac{1}{5}$,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3,
∴A3C3=$\frac{9}{4}$=($\frac{3}{2}$)2,
∴A3C3=B2C3=$\frac{9}{4}$,
∴OC3=5+$\frac{9}{4}$=$\frac{29}{4}$,
∴A3($\frac{29}{4}$,$\frac{9}{4}$),
同理可求,第四个等腰直角三角形A4C4=$\frac{27}{8}$=($\frac{3}{2}$)3,
依此类推,点An的纵坐标是($\frac{3}{2}$)n-1.
∴A2015的坐标是($\frac{3}{2}$)2014,
代入y=$\frac{1}{5}$x+$\frac{4}{5}$得,($\frac{3}{2}$)2014=$\frac{1}{5}$x+$\frac{4}{5}$,
解得x=5×($\frac{3}{2}$)2014-4,
∴A2015(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014),
故答案为:($\frac{29}{4}$,$\frac{9}{4}$),(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
| 汽车行驶时间x(h) | 0 | 1 | 2 | 3 | … |
| 剩余油量y(L) | 60 | 52 | 44 | 36 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作□ABCD,其中C、D在x轴上,则S□ABCD为( )
如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作□ABCD,其中C、D在x轴上,则S□ABCD为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,AC=2,BC=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{4π}{3}$-$\sqrt{3}$.
如图,AB是⊙O的直径,AC=2,BC=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{4π}{3}$-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com