
【题目】已知关于x的方程![]() 。
。
(1)求证:此方程总有实数根;
(2)若m为整数,且此方程有两个互不相等的负整数根,求m的值;
【答案】(1)见解析;(2)m=1.
【解析】
(1)分两种情况证明,当m=0时,此方程为4x+4=0,方程有一个实数根;当m≠0时,此方程为一元二次方程,根据根与判别式的关系即可求解;
(2)根据求根公式可得x1,x2.再根据方程有两个互不相等的负整数根,得到m=1或2或3,再进行讨论得到m的值.
(1)证明:当m=0时,此方程为4x+4=0,解得x=-1,即m=0时此方程有一个实数根;
当m≠0时,此方程为一元二次方程,
∵△=![]()
=![]() ≥0,
≥0,
∴方程总有两个实数根.
综上所述,无论m取何值方程均有实数根.
(2)解:∵![]() ,
,
∴![]() ,
,![]() .
.
∵方程有两个互不相等的负整数根,
∴![]() ,
,
∴![]() 或
或![]()
∴0<m<4。
∵m为整数,∴m=1或2或3.
当m=l时,![]() ,符合题意:
,符合题意:
当m=2时,![]() ,不符合题意;
,不符合题意;
当m=3时,![]() ,但不是整数,不符合题意.
,但不是整数,不符合题意.
∴m=1.
故答案为:(1)见解析;(2)m=1.


科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点A的坐标为(﹣4,0),B的坐标为(1,0),且OC=4OB.
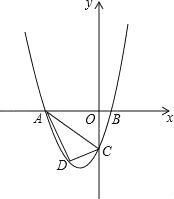
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求三角形ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是( )
A. 120°B. 125°C. 135°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
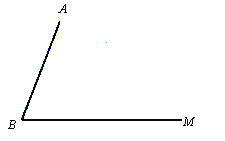
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,则树高AB=( )m.
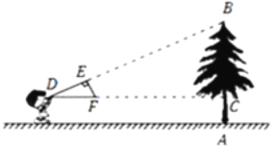
A. 3.5B. 4C. 4.5D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用力旋转如图所示的甲转盘和乙转盘的指针,如果指针停在蓝色区域就称为成功.
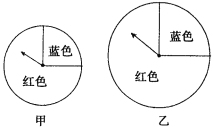
A同学说:“乙转盘大,相应的蓝色部分的面积也大,所以选乙转盘成功的机会比较大.”
B同学说:“转盘上只有两种颜色,指针不是停在红色上就是停在蓝色上,因此两个转盘成功的机会都是50%.”
你同意两人的说法吗?如果不同意,请你预言旋转两个转盘成功的机会有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,给出下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABF:S四边形CDEF=2:5,其中正确的结论有( )
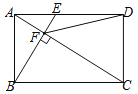
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com